经典算法

最小生成树算法

• 连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。
• 强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。
• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
• 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

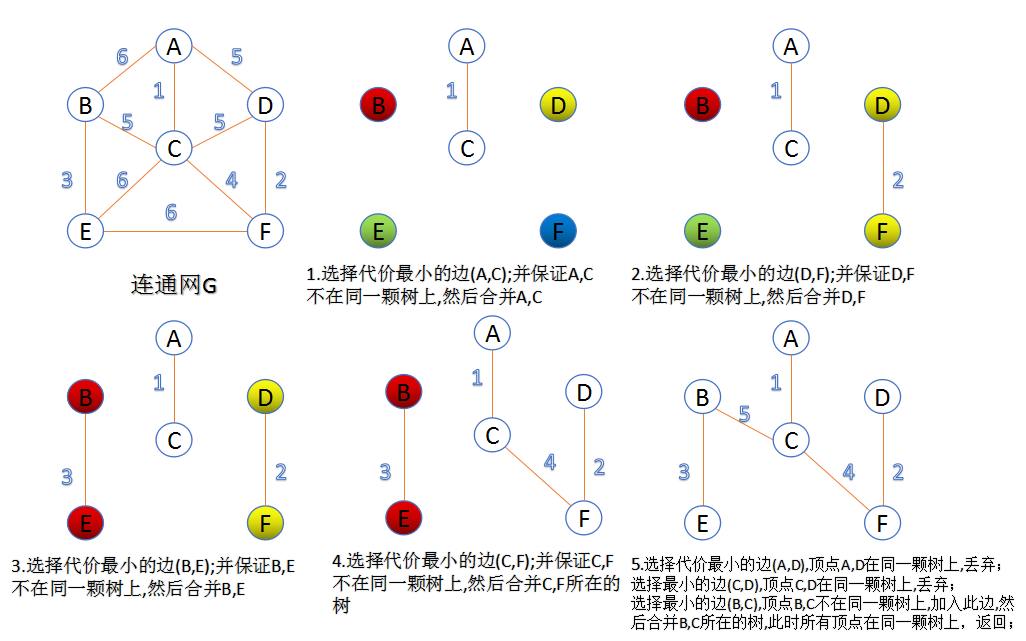
1.Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。 
1. 把图中的所有边按代价从小到大排序； 
2. 把图中的n个顶点看成独立的n棵树组成的森林； 
3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。 
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

2.Prim算法

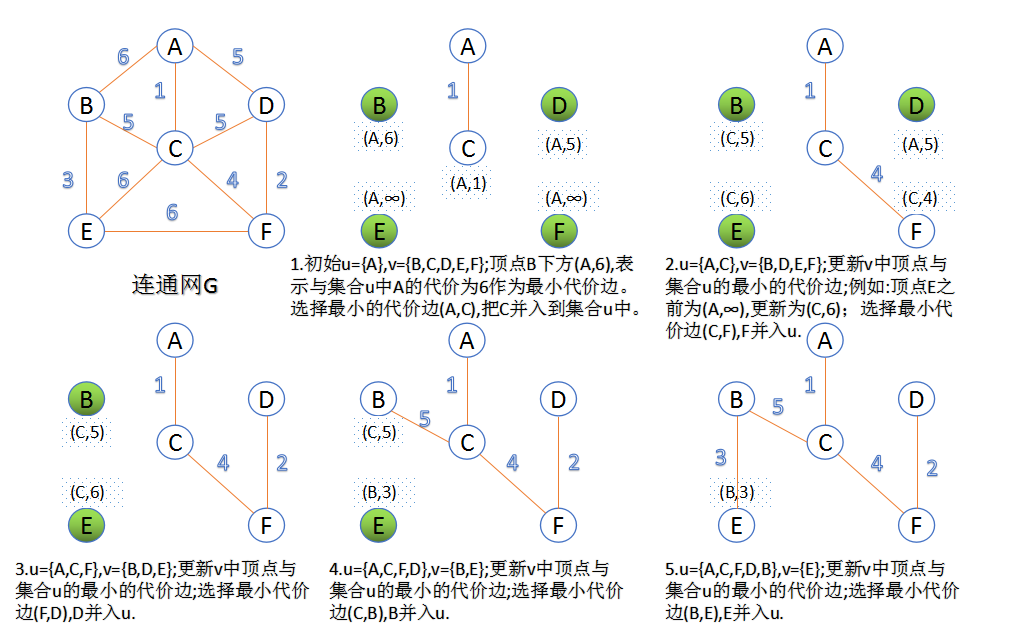
此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;
2. 在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。
3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

最短路径算法

所谓最短路径问题是指：如果从图中某一顶点（源点）到达另一顶点（终点）的路径可能不止一条，如何找到一条路径使得沿此路径上各边的权值总和（称为路径长度）达到最小。

Dijkstra（迪杰斯特拉）算法（解决单源最短路径）

划重点，迪杰斯特拉最最朴素的思想就是按长度递增的次序产生最短路径。即每次对所有可见点的路径长度进行排序后，选择一条最短的路径，这条路径就是对应顶点到源点的最短路径。

【1】不断运行广度优先算法找可见点，计算可见点到源点的距离长度

【2】从当前已知的路径中选择长度最短的将其顶点加入S作为确定找到的最短路径的顶点。

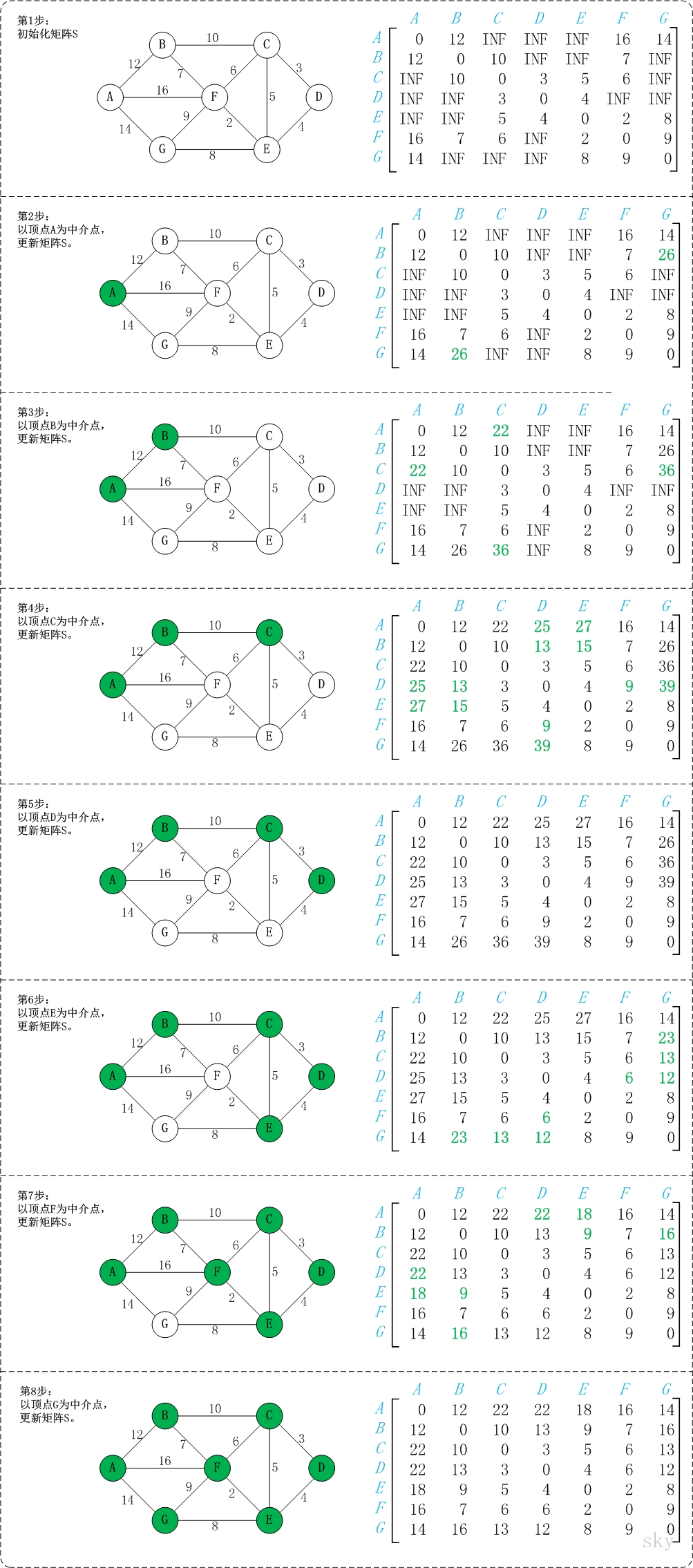
弗洛伊德算法

基本思想：
弗洛伊德算法定义了两个二维矩阵：

1. 矩阵D记录顶点间的最小路径
   例如D[0][3]= 10，说明顶点0 到 3 的最短路径为10；
2. 矩阵P记录顶点间最小路径中的中转点
   例如P[0][3]= 1 说明，0 到 3的最短路径轨迹为：0 -> 1 -> 3。

它通过3重循环，k为中转点，v为起点，w为终点，循环比较D[v][w] 和 D[v][k] + D[k][w] 最小值，如果D[v][k] + D[k][w] 为更小值，则把D[v][k] + D[k][w] 覆盖保存在D[v][w]中。

 LRU算法

什么是LRU算法？

就是一种缓存淘汰策略。

LRU 算法的设计原则是：如果一个数据在最近一段时间没有被访问到，那么在将来它被访问的可能性也很小。也就是说，当限定的空间已存满数据时，应当把最久没有被访问到的数据淘汰。

LRU 算法实际上是让你设计数据结构：首先要接收一个 capacity 参数作为缓存的最大容量，然后实现两个 API，一个是 put(key, val) 方法存入键值对，另一个是 get(key) 方法获取 key 对应的 val，如果 key 不存在则返回 -1。

注意哦，get 和 put 方法必须都是 O(1) 的时间复杂度。

 

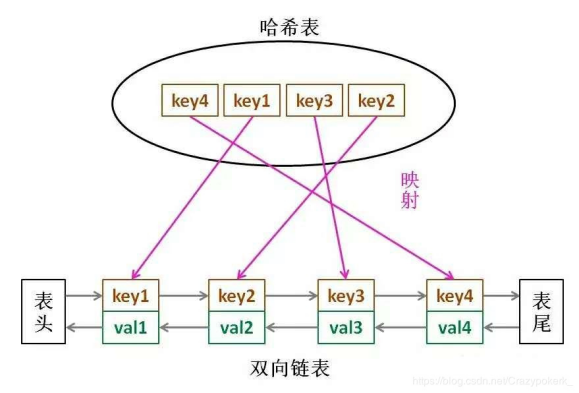
LRU 缓存算法的核心数据结构就是哈希链表，双向链表和哈希表的结合体。

蓄水池算法

 鸡蛋掉落算法

有一栋楼共100层，一个鸡蛋从第N层及以上的楼层落下来会摔破， 在第N层以下的楼层落下不会摔破。给你2个鸡蛋，设计方案找出N，并且保证在最坏情况下， 最小化鸡蛋下落的次数。

使用动态规划原理。动态规划式子如下：

f[n][m] = 1+max(f[n-1][k-1],f[n][m-k]) k属于[1,m-1] 
解释下原理： 
1、当手里有n个的时候，鸡蛋从k层往下摔，如果破了，那么手里只有n-1鸡蛋了，那么就需要测试f[n-1][k-1]楼层。或者更通俗好理解点的，我们运用2个鸡蛋100楼层的题目举例子。以上式子变为：f[2][m] = 1+max(f[1][k-1],f[2][m-k]) 
　　那么当手里有2个鸡蛋的时候，在k层摔，碎了。那么现在手里也就只有一个鸡蛋了，此时我们必须遍历1~k-1找出第一次碎的楼层。所以为1+f[1][m-k]，前面的1代表在k层的操作。 
2、没破，那么手里还有n个鸡蛋，那么需要测试k+1~m这些楼层。

此时我想问下，当手里有2个鸡蛋测试1~m-k层和手里有2个鸡蛋测试k+1~m有什么区别？ 
有人说有，因为楼层越高越容易碎，那其实是你个人的想法罢了。其实并没有区别，所以第一个公式可以写为f[n][m-k]。