poj1200 字符串hash 滚动哈希初探

假如要判断字符串A“AABA”是否是字符串B“AABAACAADAABAABA”的子串

最朴素的算法是枚举B的所有长度为4的子串，然后逐个与A进行对比，这样的时间复杂度是O(mn)，m为A的长度，n为B的长度。

另一个做法是用哈希函数计算出A的哈希值，然后计算出B所有长度为4的子串的哈希值，这样比较就可以判断出A是否在B中。虽然这样做的时间复杂度还是O(mn)，但是为接下来的滚动哈希打下了基础。

Rabin-Karp算法采用了一种叫做滚动哈希的技巧，对哈希函数的类型有要求。

Rabin-Karp算法的思想：

1. 假设待匹配字符串的长度为M，目标字符串的长度为N（N>M）；
2. 首先计算待匹配字符串的hash值，计算目标字符串前M个字符的hash值；
3. 比较前面计算的两个hash值，比较次数N-M+1：
   • 若hash值不相等，则继续计算目标字符串的下一个长度为M的字符子串的hash值
   • 若hash值相同，则需要使用朴素算法再次判断是否为相同的字串；

哈希函数定义如下。

其中Cm表示字符串中第m项所代表的特地数字，有很多种定义方法，我习惯于用java自带的char值，也就是ASCII码值。java中的char是16位的，用的Unicode编码，8位的ASCII码包含在Unicode中。

b是哈希函数的基数，相当于把字符串看作是b进制数。

h是防止哈希值溢出。

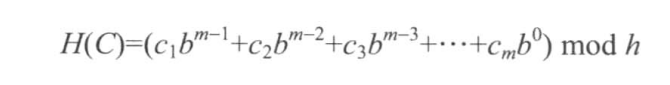
滚动哈希的技巧就是：如果已经算出从k到k+m的子串的哈希值H(S[k,k+1...k+m])，那么从k+1到k+m+1的子串的哈希值就可以基于前一个的哈希值计算得出

 在不考虑哈希碰撞的前提下，Rabin-Karp算法的时间复杂度就是O(m+n)。

那么来看看POJ 1200

题目大意是有一个字符串，其中有NC种不同的字符，求出其长度为N的不同子串的个数。

这个题目的本意是要利用这个NC，但是我这里只是为了训练滚动哈希，就没有用NC。可以把哈希函数的基数b设为NC，就相当于把字符串转换成了NC进制

 

import java.util.HashSet;
import java.util.Scanner;


public class test {

    static long pat;    //原始长度为n的子串的哈希值
    static long next;   //右移一位子串的哈希值
    static long B = 100000007;  //哈希函数基数
    static long max = Integer.MAX_VALUE;    //取模防止哈希值溢出

    public static void main(String[] args) {
        
        HashSet<Long> res = new HashSet<Long>();    //把子串的哈希值放入hashset中，hashset的size就是所求子串个数
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt();
        int nc = scanner.nextInt();
        scanner.nextLine();
        String buff = scanner.nextLine();
        char[] s = buff.toCharArray();

        long t = 1;
        
        //计算出B的n次方
        for (int i = 0; i < n; i++) {
            t = (t * B) % max;
        }
        
        //计算出第一个子串的哈希值
        for (int i = 0; i < n; i++) {
            pat = (pat * B + s[i]) % max;
        }
        next = pat;
        res.add(next);
        
        //没有考虑哈希冲突，直接右移计算
        for (int i = 0; i + n < s.length; i++) {
            next = (next * B + s[i + n] - s[i] * t) % max;
            res.add(next);
        }
        
        System.out.println(res.size());
    }
}