A Fence standard input/output 1 s, 256 MB Submit Add to favourites x14752
//https://www.quora.com/How-do-I-find-the-fourth-side-of-quadrilateral-if-three-sides-are-given
// how to find the fourth side
// we can first pick the max side of the given three sides
// then draw the line segment in the picture like AB
// and Use the two endpoints of this line segment as the centers of the two circles(their radius is the other given sides)
// when we draw two circles we will find the maximum of fourth side is when the two circles are as far apart as possible and the minimum is when the two circles are as close as possible
// so min(a,b,c,d) > max(1, c-a-b) and max(a,b,c,d) < a+b+c+d-max(a,b,c,d) (assume c is max(a,b,c))
// 假设 c 是三条边里最长的边
// 在纸上画出c长度的线段AB 然后以A B分别作圆且半径为a、b
// 然后会发现第四条最大的情况是两个圆周上的点离得尽可能远 最小的情况是两个圆周上的点离得尽可能近
// 如下图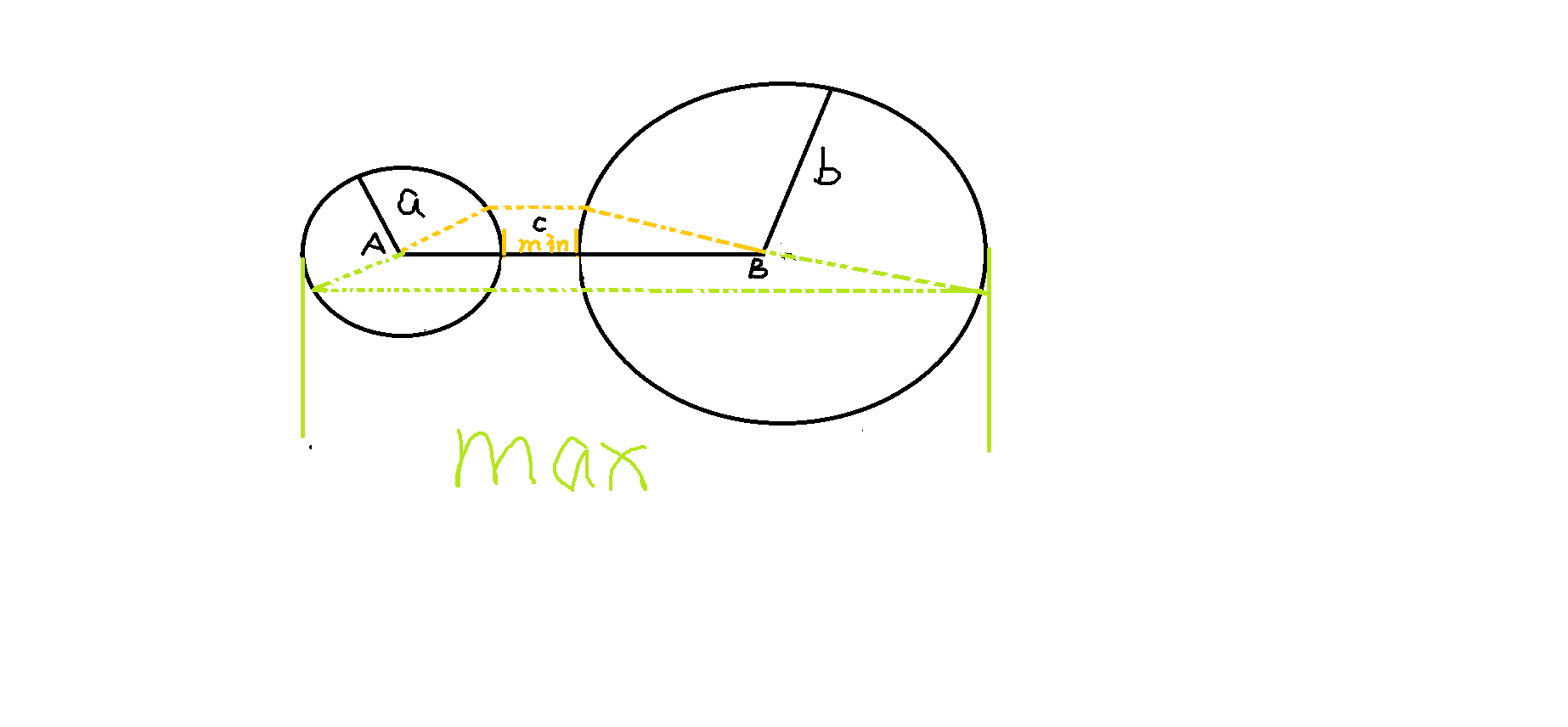
B Nice Matrix standard input/output 1 s, 256 MB Submit Add to favourites x9064
// 所有的行和列都需要成为回文串, 所以观察一下会发现 每个长方形的四个角的数字必须相同,所以枚举所有的四个点 取中位数作为回文串数字 然后累积差值之和即可
// 至于为什么取的是中位数 则是之前在紫薯上看到的理论 一条线段上4四个点 找一个点到四个点的距离和最小 取中间两个点中的任意点即可
C Bargain standard input/output 1 s, 256 MB Submit Add to favourites x4953
// 开始想的是从m个数字中选取k个数字组成的数字之和( m<1e5 k<=9), 然而(1e5)^9 这也顶不住啊
// 然后题解出了以后看了题解 从后往前枚举每个位置的贡献, 当这个位置的右边数字被删除时, 它的贡献是 10^(n-i-1) *(n-i)的累积, 当这个位置的左边数字被删除时 他的贡献为 (i*(i+1))
// 所以遍历一遍,预处理右边贡献 到当前位置时 加上左边贡献 再乘上该位置的数字值即可
D Returning Home standard input/output 2 s, 256 MB Submit Add to favourites x1660
// 把所有的快速点暴力枚举下两两快速点之间的步数,记录下两个快速点的最短距离,然后遍历下 取 从快速点到终点与快速点到起点之和的最小值
#include <bits/stdc++.h> using namespace std; #define _for(i,a,b) for(int i = (a); i < (b); i++) #define _rep(i,a,b) for(int i = (a); i <= (b); i++) #define all(v) (v).begin(), (v).end() #define ll long long
void taskA() { int t; cin >> t; while(t--) { int a,b,c,d; cin >> a >> b >> c; //cout << max(a, max(b, c)) << " "; // or a+b+c-1 maxnal max(a,b,c,d) < a+b+c+d-max(a,b,c,d) int e = max(a, max(b, c)); if(e > a+b+c-e) cout << e-(a+b+c-e)+1 << " "; // minal else cout << "1 "; } return; }
const int N = 100+10; const int MOD = 1e9+7; int a[N][N], vis[N][N]; void taskB() { int t; cin >> t; while(t--) { int n,m; cin >> n >> m; memset(vis, 0, sizeof vis); _for(i,0,n) _for(j,0,m) cin >> a[i][j]; ll ans = 0; _for(i,0,n) _for(j,0,m) { //cout << " ans = " << ans << " "; if(!vis[i][j]) { //if(i == n-1-i || j == m-1-j) continue; vector<int> d{a[i][j]}; vis[i][j] = 1; if(m-1-j >= 0 and !vis[i][m-1-j] and j != m-1-j) d.push_back(a[i][m-1-j]), vis[i][m-1-j] = 1; if(n-1-i >= 0 and !vis[n-1-i][j] and i != n-1-i) d.push_back(a[n-1-i][j]), vis[n-1-i][j] = 1; if(m-1-j >= 0 and n-1-i >= 0 and !vis[n-1-i][m-1-j] and i != n-1-i and m-1-j) d.push_back(a[n-1-i][m-1-j]), vis[n-1-i][m-1-j] = 1; sort(all(d)); int sz = d.size(); _for(k,0,sz) ans += abs(d[k]-d[sz/2]); } //cout << "ans = " << ans << " "; } //if(n&1) {_for(j,0,m/2) ans += abs(a[n/2][m-1-j]-a[n/2][j]);} //if(m&1) {_for(i,0,n/2) ans += abs(a[i][n/2]-a[n-1-i][n/2]);} cout << ans << " "; } return; }
ll calc(vector<ll>& a) { sort(all(a)); int sz = a.size(); ll ret = 0; _for(i,0,sz) ret += abs(a[i]-a[sz/2]); return ret; } void taskB1() { int t; cin >> t; while(t--) { int n,m; ll ans = 0; cin >> n >> m; int matrix[110][110] = {}; _for(i,0,n) _for(j,0,m) cin >> matrix[i][j]; int up_row = 0, bottom_row = n-1; while(up_row <= bottom_row) { int left_column = 0, right_column = m-1; while(left_column <= right_column) { vector<ll> num{matrix[up_row][left_column]}; if(up_row != bottom_row) num.push_back(matrix[bottom_row][left_column]); if(left_column != right_column) num.push_back(matrix[up_row][right_column]); if(up_row != bottom_row and left_column != right_column) num.push_back(matrix[bottom_row][right_column]); ans += calc(num); left_column++, right_column--; } up_row++, bottom_row--; } cout << ans << " "; } return; }
void taskC() { string s; cin >> s; int n = s.size(); ll sum = 0, p = 1, k = 0, ans = 0; for(ll i = n-1; i >= 0; i--) { k = (i*(i+1)/2*p+sum)%MOD; sum = (sum+p*(n-i))%MOD; p = p*10%MOD; ans = (ans+(s[i]-'0')*k%MOD)%MOD; } cout << ans << " "; return; }
template <typename T> bool chmin(T &x, const T& y) {return x>y ? x = y, true : false;} template <typename T> bool chmax(T &x, const T& y) {return x<y ? x = y, true : false;} void taskD() { int _, n; cin >> _ >> n; int sx, sy, fx, fy; cin >> sx >> sy >> fx >> fy; vector<tuple<int, int, int>> a(n), b(n); vector<pair<int, int>> p; _for(i,0,n) { int x, y; cin >> x >> y; int d = min(abs(sx-x), abs(sy-y)); p.push_back({x, y}); a[i] = make_tuple(x, y, i); //保存快速点 b[i] = make_tuple(y, x, i); } vector<vector<pair<int, int>>> e(n); auto bt = [&](vector<tuple<int, int, int>> &s) { sort(all(s)); // 枚举任意两个快速点的最短距离 _for(i,1,n) { int x1, y1, u, x2 ,y2, v; tie(x1, y1, u) = s[i-1]; tie(x2, y2, v) = s[i]; int d = min(abs(x1-x2), abs(y1-y2)); e[u].push_back({v, d}); e[v].push_back({u, d}); } }; bt(a), bt(b); vector<ll> d(n); priority_queue<vector<pair<ll, int>>, vector<pair<ll, int>>, greater<pair<ll, int>>> q; _for(i,0,n) { d[i] = min(abs(sx-p[i].first), abs(sy-p[i].second)); q.push({d[i], i});// 将起点到快速点距离记录 } while(!q.empty()) { ll w; int x; tie(w, x) = q.top(); q.pop(); if(d[x] != w) continue; for(auto u : e[x]) { ll y = u.first; int c = u.second; if(chmin(d[y], w+c)) // 通过在快速点与快速点之间 横跳 来找到起点到快速点的最小距离(bfs q.push({d[y], y}); } } ll ans = abs(sx-fx)+abs(sy-fy); _for(i,0,n) chmin(ans, d[i]+abs(fx-p[i].first)+abs(fy-p[i].second)); // 找到最小的 起点到快速点加快速点到终点之和 的距离 cout << ans << " "; return; }
int main() { ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr); #ifdef LOCAL assert(freopen("i.txt", "r", stdin)); assert(freopen("o.txt", "w", stdout)); #endif taskD(); //taskC(); #ifdef LOCAL cerr << "Time execute: " << clock() / (double)CLOCKS_PER_SEC << " sec" << endl; #endif return 0; }