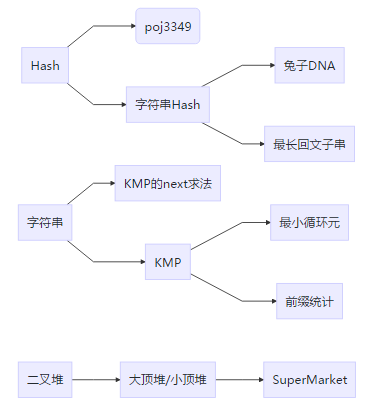
一.Hash
Smowflake Snow Snowflakes(poj3349)
题意:给几组数字,每组都只有6个,判断是否存在顺时针或者逆时针相同顺序遍历的两组数字。
坑:按照书上的hash方法始终TL,但是还没有研究出来这是为什么。
const int SIZE = 100010;
int n,tot,p = 99991;
int snow[SIZE][6],head[SIZE],nxt[SIZE];
int H(int *a)
{
int sum = 0,mul = 1;
for(int i=0;i<6;i++){
sum = (sum+a[i])%p;
//mul = (long long)mul*a[i]%p;
}
return (sum)%p;
}
bool equal(int *a,int *b)
{
for(int i=0;i<6;i++)
{
for(int j=0;i<6;j++)
{
bool eq = 1;
for(int k=0;k<6;k++)
if(a[(i+k)%6]!=b[(j+k)%6])
eq = 0;
if(eq)
return 1;
eq = 1;
for(int k=0;k<6;k++)
if(a[(i+k)%6]!=b[(j-k+6)%6])//反向检测
eq = 0;
if(eq)
return 1;
}
}
return 0;
}
bool insert(int *a)
{
int val = H(a);
//cout<<val<<endl;
for(int i=head[val];i;i=nxt[i])
{
//cout<<i<<endl;
if(equal(snow[i],a))
return 1;
}
++tot;
memcpy(snow[tot],a,sizeof(int)*6);
nxt[tot] = head[val];
head[val] = tot;
return 0;
}
int main()
{
cin>>n;
//tot =0;
//memset(nxt,0,sizeof nxt);
for(int i=0;i<n;i++)
{
int a[10];
for(int j=0;j<6;j++)
scanf("%d",&a[j]);
if(insert(a))
{
puts("Twin snowflakes found.");
return 0;
}
}
puts("No two snowflakes are alike.");
return 0;
}
字符串Hash
方法:把字符串当做一个p进制数,p一般取131或者13331,直接用ull储存这个Hash值,因为溢出相当于自动对2^64取模,所以不用单独取模。
- 对于已知的S的Hash值为H[s],若在后面添加一个字符c构成新字符串S+c的哈希值就是
H(s+c) = (H[s]*p+value[c])%M - 如果已知S的Hash值H[s],字符串s+t的Hash值为H(S+t),那么字符串t的Hash值
H(t) = (H(s+t)-h(s)*p^(length(t)))%M
兔子与兔子
很久很久以前,森林里住着一群兔子。有一天,兔子们想要研究自己的 DNA 序列。我们首先选取一个好长好长的 DNA 序列(小兔子是外星生物,DNA 序列可能包含 26 个小写英文字母),然后我们每次选择两个区间,询问如果用两个区间里的 DNA 序列分别生产出来两只兔子,这两个兔子是否一模一样。注意两个兔子一模一样只可能是他们的 DNA 序列一模一样。
char s[1000001];
long long h[1000001],p[1000001];
int m,l1,r1,l2,r2;
int main()
{
scanf("%s",s+1);
int n = strlen(s+1);
p[0] = 1,h[0] = 0;
for(int i=1;i<=n;i++)
{
h[i] = h[i-1]*131+(s[i]-'a'+1);
p[i] = p[i-1]*131;
}
scanf("%d",&m);
for(int i=0;i<m;i++)
{
scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
if(r1-l1!=r2-l2)
{
puts("No");
continue;
}
//if((h[r1]-h[l1-1])/p[l1-1]==(h[r2]-h[l2-1])/p[l2-1])
if(h[r1]-h[l1-1]*p[r1-l1+1]==h[r2]-h[l2-1]*p[r2-l2+1])
puts("Yes");
else
puts("No");
}
return 0;
}
Pailindrome(poj3974)
题意:给一个字符串,求最长回文子串
O(nlog(n))方法,还有一个Manacher的算法可以O(n)解决,不过我还没去看
#define MAX 1000010
char s[MAX];
long long h1[MAX],h2[MAX],p[MAX];
int ans;
int n;
bool check(int i,int len,int model)
{
if(model==1)
{
if(i-1<len||n-i+1<len)
return false;
if(h1[i-1]-h1[i-len-1]*p[len]==h2[i+1]-h2[i+1+len]*p[len])
return true;
else
return false;
}
if(model==2)
{
if(i<len||n-i+1<len)
return false;
if(h1[i]-h1[i-len]*p[len]==h2[i+1]-h2[i+1+len]*p[len])
return true;
else
return false;
}
return false;
}
int main()
{
int cas = 0;
while(scanf("%s",s+1))
{
if(s[1] =='E')
break;
n = strlen(s+1);
if(n==1)
{
printf("Case %d: 1
",++cas);
continue;
}
p[0] = 1,h1[0] = 0,h2[0] = 0;
for(int i=1;i<=n;i++)
{
h1[i] = h1[i-1]*131+s[i]-'a'+1;
p[i] = p[i-1]*131;
}
h2[n+1] = 0;
for(int i=n;i>=1;i--)
{
h2[i] = h2[i+1]*131+s[i]-'a'+1;
}
ans = 0;
for(int i=1;i<=n;i++)
{
int l = 1,r = n;
while(l<r)
{
int mid = (l+r+1)>>1;
//cout<<l<<r<<mid<<endl;
if(check(i,mid,1))
l=mid;
else
r = mid-1;
}
ans = max(ans,2*l+1);
l = 1,r=n;
while(l<r)
{
int mid = (l+r+1)>>1;
if(check(i,mid,2))
l=mid;
else
r = mid-1;
}
ans = max(ans,l*2);
}
printf("Case %d: %d
",++cas,ans);
}
return 0;
}
字符串
KMP
#define LEN 1001;
char s[1001];
int nxt[1001];
void getNext_1()//最常见的kmp的next求法,适用于表示不包含当前字符的前缀与后缀匹配
{
int j=1,len = strlen(s),k=-1;
nxt[0] = -1;
while(j<len-1)
{
if(k==-1||(s[j]==s[k]))
{
nxt[++j] = ++k;
}
else
{
k = nxt[k];
}
}
}
void getNext_2()
{
int len = strlen(s+1);
//====下标从1开始====//
nxt[1] = 0;
for(int i=2,j=0;i<=len;i++)
{
while(j>0&&s[i]!=s[j+1])
j=nxt[j];
if(s[i]==s[j+1])
j++;
nxt[i] = j;
}
//================/*/
/*/====下标从0开始====//
nxt[0] = -1;
for(int i=1,j=-1;i<len;i++)
{
while(j>=0&&s[i] != s[j+1])
j=nxt[j];
if(s[i]==s[j+1])
j++;
nxt[i] = j;
}
//================/*/
}
Period(POJ1961)
题意:如果一个字符串S是由一个字符串T重复K次形成的,则称T是S的循环元。使K最大的字符串T称为S的最小循环元,此时的K称为最大循环次数。
现在给定一个长度为N的字符串S,对S的每一个前缀S[1~i],如果他的最大循环次数大于1,则输出该前缀的最小循环元长度和最大循环次数。
#define LEN 1000010
char s[LEN];
int nxt[LEN];
int n;
void calc_nxt()
{
nxt[1] = 0;
for(int i=2,j=0;i<=n;i++)
{
while(j>0&&s[i]!=s[j+1])
j = nxt[j];
if(s[i] == s[j+1])
j++;
nxt[i] = j;
}
}
int main()
{
int cas = 0;
while(cin>>n,n)
{
scanf("%s",s+1);
calc_nxt();
printf("Test case #%d
",++cas);
for(int i=2;i<=n;i++)
{
if(i%(i-nxt[i])==0&&i/(i-nxt[i])>1)
{
printf("%d %d
",i,i/(i-nxt[i]));
}
}
puts("");
}
return 0;
}
前缀统计(CH1601)
题意:给定N个字符串S1,S2...SN,接下来进行M次询问,每次询问给定一个字符串T,求S1~SN中有多少个字符串是T的前缀。输入字符串的总长度不超过10^6,仅包含小写字母。
#define SIZE 100001
struct node
{
int nxt;
int cnt;
}trie[SIZE][26];
char s[100001];
int tot=1;
int n,m;
void insert(char* str)
{
int len = strlen(str),p=1;
for(int k=0;k<len;k++)
{
int ch = str[k]-'a';
if(trie[p][ch].nxt==0)
{
trie[p][ch].nxt = ++tot;
}
if(k==len-1)
trie[p][ch].cnt++;
p=trie[p][ch].nxt;
}
}
int search(char *str)
{
int p = 1,num = 0;
int len = strlen(str);
for(int i=0;i<len;i++)
{
int ch = str[i]-'a';
if(trie[p][ch].nxt!=0)
{
num+=trie[p][ch].cnt;
p = trie[p][ch].nxt;
}
else
break;
}
return num;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
scanf("%s",s);
insert(s);
}
for(int i=0;i<m;i++)
{
scanf("%s",s);
cout<<search(s)<<endl;
}
return 0;
}
二叉堆
大顶堆
int heap[SIZE],n;
void up(int p)
{
while(p>1)
{
if(heap[p]>heap[p/2])
{
swap(heap[p],heap[p/2]);
p/=2;
}
else
break;
}
}
void insert(int val)
{
heap[++n] = val;
up(n);
}
int getTop()
{
return heap[1];
}
void down(int p)
{
int s = p*2;
while(s<=n)
{
if(s<n&&heap[s]<heap[s+1])s++;
if(heap[s]>heap[p])
{
swap(heap[s],heap[p]);
p = s;
s = s*2;
}
else
break;
}
}
void Extract()
{
heap[1] = heap[n--]
down(1);
}
void remove(int k)
{
heap[k] = heap[n--];
up(k),down(k);
}
Surpermarket(poj1456)
题意:有n个商品,每个商品有利润和过期天数。每天只能卖一个,求最大利润。
分析:
- 肯定是要把所有的商品都卖完的。但是当确定某一天时,要尽量让利润更大,所以要使每一天卖的商品都是最大利润的。
- 首先要保证不过期,所以要先考虑过期天数少的。所以按照天数从小到大排序。
- 然后从小的开始添加进最小堆,如果当前物品的过期天数大于堆的大小,则直接添加进堆中,如果当前物品过期天数(days)与堆的大小一致,那么意思也就是说前days天都有卖的了,那就要用当前物品的利润与堆顶元素的利润作比较。然后做出调整。舍弃某一物品
- 最后堆中元素就是要卖的物品
1.自己构造最小堆
#define SIZE 10001
struct node
{
int val;
int days;
}heap[SIZE],tmp[SIZE];
int n,s;
void up(int p)
{
while(p>1)
{
if(heap[p].val<heap[p/2].val)
{
swap(heap[p],heap[p/2]);
p/=2;
}
else
break;
}
}
void insert(int val,int days)
{
heap[++n].val = val;
heap[n].days = days;
up(n);
}
void down(int p)
{
int s = p*2;
while(s<=n)
{
if(s<n&&heap[s].val>heap[s+1].val)s++;
if(heap[s].val<heap[p].val)
{
swap(heap[s],heap[p]);
p = s;
s = s*2;
}
else
break;
}
}
void extract()
{
heap[1].val = heap[n].val;
heap[1].days =heap[n--].days;
down(1);
}
int getTop()
{
return heap[1].val;
}
bool cmp(node a,node b)
{
return a.days<b.days;
}
int main()
{
while(cin>>s)
{
n = 0;
for(int i=1;i<=s;i++)
{
scanf("%d%d",&tmp[i].val,&tmp[i].days);
}
sort(tmp+1,tmp+1+s,cmp);
for(int i=1;i<=s;i++)
{
if(tmp[i].days>n)
insert(tmp[i].val,tmp[i].days);
else if(tmp[i].days==n)
{
int tmp_val = getTop();
if(tmp_val<tmp[i].val)
{
extract();
insert(tmp[i].val,tmp[i].days);
}
}
}
int ans = 0;
for(int i=1;i<=n;i++)
{
ans += heap[i].val;
}
cout<<ans<<endl;
}
return 0;
}
2.利用STL优先队列实现
#define SIZE 100001
struct node{
int val,days;
bool operator<(const node& tmp)const
{
return val>tmp.val;
}
}a[SIZE];
bool cmp(node a,node b)
{
return a.days<b.days;
}
int main()
{
int n;
while(cin>>n)
{
for(int i=0;i<n;i++)
scanf("%d%d",&a[i].val,&a[i].days);
sort(a,a+n,cmp);
priority_queue<node> q;
for(int i=0;i<n;i++)
{
if(a[i].days>q.size())
{
q.push(a[i]);
}
else if(a[i].days==q.size())
{
node tmp = q.top();
if(tmp.val<a[i].val)
{
q.pop();
q.push(a[i]);
}
}
}
int ans = 0;
while(!q.empty())
{
node tmp = q.top();
ans += tmp.val;
q.pop();
}
cout<<ans<<endl;
}
return 0;
}