1、二叉树(binary)

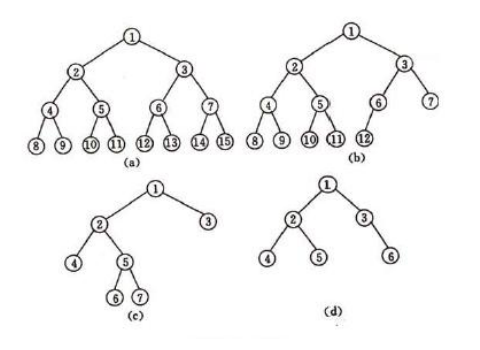
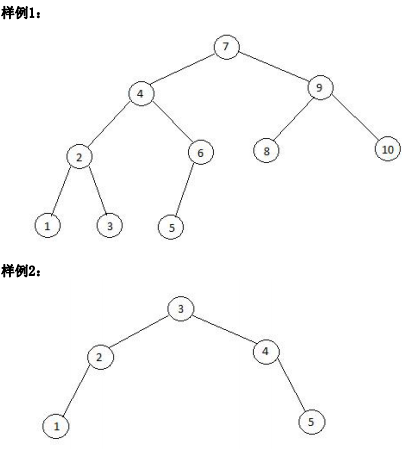
1.二叉树 (binary.cpp/c/pas) 【问题描述】 二叉排序树或者是一棵空树,或者是具有下列性质的二叉树: (1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值; (2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值; (3)左、右子树也分别为二叉排序树; (4)没有键值相等的结点。 完全二叉树:只有最下面的两层结点度能够小于2,并且最下面一层的结点 都集中在该层最左边的若干位置的二叉树。 图1中,(a)和(b)是完全二叉树,(c)和(d)是非完全二叉树。 给出N个数,且这N个数构成1至N的排列。现在需要你按顺序构建一棵二叉 排序树,并按照层次遍历的方式输出它,然后判断它是否是一棵完全二叉树。 【输入格式】 输入文件名为binary.in。 输入文件包含两行。第一行为一个正整数N;第二行为1至N的排列。 【输出格式】 输出文件名为binary.out。 输出文件包含两行。第一行为构建出的二叉排序树的层次遍历;第二行判 断是否是完全二叉树:若是输出yes,否则输出no。 【输入输出样例1】 binary.in 10 7 9 8 4 6 2 10 1 5 3 binary.out 7 4 9 2 6 8 10 1 3 5 yes 【输入输出样例2】 binary.in 5 3 4 5 2 1 binary.out 3 2 4 1 5 no 【数据规模与约定】 对于100%的数据,1≤N≤20。
tag:模拟
思路:其实这道题没有看上去那么复杂。插入的时候比节点大就往右走,反之往左走,走到头了放进去,最后建个树。判断是不是完全二叉树要看最大的节点是不是在自己应该在的位置,因为仔细观察发现完全二叉树是每一层从左往右一个一个放,每个节点的数值和编号应该相等(感谢dalao这句话的思路)。
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #include<queue> 6 using namespace std; 7 int maxx,list[30][30],tree[1<<21],deep,n; 8 void insert(int o,int x) 9 { 10 maxx=max(maxx,o); 11 if(!tree[o]){ 12 tree[o]=x; 13 return; 14 } 15 if(x>tree[o]) insert(o<<1|1,x); 16 else insert(o<<1,x); 17 } 18 void dfs(int o,int f) 19 { 20 deep=max(deep,f); 21 if(tree[o<<1]){ 22 list[f+1][++list[f+1][0]]=tree[o<<1]; 23 dfs(o<<1,f+1); 24 } 25 if(tree[o<<1|1]){ 26 list[f+1][++list[f+1][0]]=tree[o<<1|1]; 27 dfs(o<<1|1,f+1); 28 } 29 } 30 int main() 31 { 32 //freopen("binary.in","r",stdin); 33 //freopen("binary.out","w",stdout); 34 int x; 35 scanf("%d",&n); 36 for(int i=1;i<=n;++i){ 37 scanf("%d",&x); 38 insert(1,x); 39 } 40 list[1][1]=tree[1]; 41 list[1][0]=1; 42 dfs(1,1); 43 for(int i=1;i<=deep;++i) 44 for(int j=1;j<=list[i][0];++j) 45 printf("%d ",list[i][j]); 46 puts(""); 47 if(maxx!=n) puts("no"); 48 else puts("yes"); 49 return 0; 50 }
2、列车调度(manage)

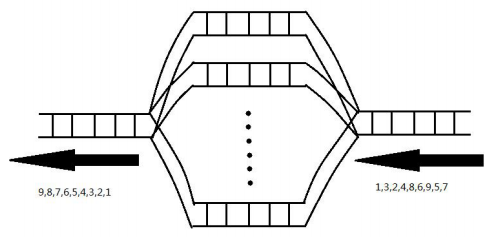
【问题描述】 有N辆列车,标记为1,2,3,…,N。它们按照一定的次序进站,站台共有K个轨 道,轨道遵从先进先出的原则。列车进入站台内的轨道后可以等待任意时间后出 站,且所有列车不可后退。现在要使出站的顺序变为N,N-1,N-2,…,1,询问K的 最小值是多少。 例如上图中进站的顺序为1,3,2,4,8,6,9,5,7,则出站的顺序变为 9,8,7,6,5,4,3,2,1。 【输入格式】 输入文件名为manage.in。 输入共2行。 第 1 行包含1个正整数N,表示N辆列车。 第 2 行包含N个正整数,为1至N的一个排列,表示进站次序。 【输出格式】 输出文件名为manage.out。 输出共1行,包含1个整数,表示站台内轨道数K的最小值。 【输入输出样例1】 manage.in 3 1 2 3 manage.out 3 【输入输出样例2】 manage.in 9 1 3 2 4 8 6 9 5 7 manage.out 5 【数据规模与约定】 对于 30%的数据,N≤10; 对于 70%的数据,N≤2000; 对于 100%的数据,N≤100000。
tag:二分查找
思路:单纯模拟用时较长(但是O(n2)居然能过???),正解是构造非降序列,比如现在的序列是(5,6,9,11),要把10插入进去,5,6,9都比10小,11比10大就停在11后面,序列变成(5,6,9,10),虽然单个的数值改变了,但是原本的单调性没变,因此我们可以二分查找第一个比要插入的数大的数(0011型)。
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #include<queue> 6 #include<cstdlib> 7 #define maxn 100010 8 using namespace std; 9 int n,a[maxn],f[maxn],ans=1; 10 int main() 11 { 12 //freopen("manage.in","r",stdin); 13 //freopen("manage.out","w",stdout); 14 scanf("%d",&n); 15 for(int i=1;i<=n;++i) scanf("%d",&a[i]); 16 f[1]=a[1]; 17 for(int i=2;i<=n;++i){ 18 int l=lower_bound(f+1,f+ans+1,a[i])-f; 19 f[l]=a[i]; 20 ans=max(ans,l); 21 } 22 printf("%d",ans); 23 return 0; 24 }
3、保留道路(road)

【问题描述】 很久很久以前有一个国家,这个国家有N个城市,城市由1,2,3,…,N标号, 城市间有M条双向道路,每条道路都有两个属性g和s,两个城市间可能有多条道 路,并且可能存在将某一城市与其自身连接起来的道路。后来由于战争的原因, 国王不得不下令减小花费从而关闭一些道路,但是必须要保证任意两个城市相互 可达。 道路花费的计算公式为wG*max{所有剩下道路的属性g}+wS*max{所有剩下道 路的属性s},其中wG和wS是给定的值。国王想要在满足连通性的前提下使这个花 费最小,现在需要你计算出这个花费。 【输入格式】 输入文件名为road.in。 第一行包含两个正整数N和M。 第二行包含两个正整数wG和wS。 后面的M行每行描述一条道路,包含四个正整数u,v,g,s,分别表示道路连接 的两个城市以及道路的两个属性。 【输出格式】 输出文件名为road.out。 输出一个整数,表示最小花费。若无论如何不能满足连通性,输出-1。 【输入输出样例】 road.in 3 3 2 1 1 2 10 15 1 2 4 20 1 3 5 1 road.out 30 【数据规模与约定】 对于 10%的数据,N≤10,M≤20; 对于 30%的数据,N≤100,M≤1000; 对于 50%的数据,N≤200,M≤5000; 对于 100%的数据,N≤400,M≤50000,wG,wS,g,s≤1000000000。
tag:最小生成树、轻度玄学(雾)
思路:二维费用的kruskal,很有研究的价值。平时我们做的最小生成树都只有一维,突然多了一个维度,而且还有系数,有点让人手足无措,我们应当以什么标准来选择,加和?乘积?比值?都不行吧,可以随便举反例。正解是,两个权值g,s任选其一作为标准从小到大排序,比如选择g就以g的大小排,再看s的大小,我们造一个栈,从底到顶s从小到大,每放一条边调整栈中各边的位置,做一遍kruskal,记录答案,时间复杂度是O(nm)。
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #include<queue> 6 #define maxn 100010 7 #define ll long long 8 #define inf 1ll<<60 9 using namespace std; 10 int gmax,smax,n,m,G,S,fa[maxn],st[maxn],top,tot; 11 ll ans=inf; 12 struct Edge{ 13 int u,v,g,s; 14 }e[maxn]; 15 bool cmp(Edge x,Edge y) 16 { 17 return x.g<y.g; 18 } 19 int find(int x) 20 { 21 return x==fa[x]?x:fa[x]=find(fa[x]); 22 } 23 int main() 24 { 25 //freopen("road.in","r",stdin); 26 //freopen("road.out","w",stdout); 27 int u,v,g,s; 28 scanf("%d%d",&n,&m); 29 scanf("%d%d",&G,&S); 30 for(int i=1;i<=m;++i) scanf("%d%d%d%d",&e[i].u,&e[i].v,&e[i].g,&e[i].s); 31 sort(e+1,e+m+1,cmp); 32 for(int i=1;i<=m;++i){ 33 int j=0; 34 for(j=1;j<=n;++j) fa[j]=j; 35 for(j=top;j>=1;--j) 36 if(e[st[j]].s>e[i].s) 37 st[j+1]=st[j]; 38 else break; 39 top++; 40 st[j+1]=i; 41 tot=0; 42 for(j=1;j<=top;++j) 43 { 44 int k1=find(e[st[j]].u),k2=find(e[st[j]].v); 45 if(k1!=k2){ 46 fa[k1]=k2; 47 st[++tot]=st[j]; 48 } 49 if(tot==n-1) break; 50 } 51 if(tot==n-1) ans=min(ans,1ll*e[i].g*G+1ll*e[st[n-1]].s*S); 52 top=tot; 53 } 54 if(ans==inf) printf("-1"); 55 else printf("%I64d",ans); 56 return 0; 57 }
————————————————懒得打分割线啊——————————————————
芒果君:考了这么多次,这场翻车最厉害,都倒数了QAQ 还是想太多
