题目背景
大芳有一个不太好的习惯:在车里养青蛙。青蛙在一个n厘米(11n毫米s)的Van♂杆子上跳来跳去。她时常盯着青蛙看,以至于突然逆行不得不开始躲交叉弹。有一天他突发奇想,在杆子上每1厘米为一个单位,瞎涂上了墨水,并且使用mOgic,使青蛙跳过之处墨水浓度增加x。当然,他还会闲着无聊滴几滴墨水再涂♂抹均匀。
他现在无时无刻都想知道,第l厘米到第r厘米墨水的浓度是多少?
哦不!等等,他现在找到了一个计算器,可以输入几个数字与x,计算他们的x次幂和,所以。。。他想知道的是第l厘米到第r厘米墨水的浓度的x次幂和是多少?
题目描述
大芳有3种舰长技能骚操作
-
续:把青蛙放到第l厘米处,戳青蛙使其跳至r。效果:第l厘米至第r厘米墨水浓度增加x
- 抚♂摸:擦干杆子某一部分,重新滴加墨水并抹匀。效果:使第l厘米至第r厘米墨水浓度都变成x
最后一种是:
- 压线逆行,将车流看做⑨弹幕找安定点,掏出计算器,大喊板载后计算:
第l厘米至第r厘米墨水浓度的x次幂和是几何?记得答案要
模10000000071000000007
输入输出格式
输入格式:
第一行nn和mm,表示杆子长n厘米,大芳要进行m次骚操作。
第二行nn个数字,表示初始墨水浓度。第i个数字为第i厘米墨水浓度
接下来每行4个数字,依次为:操作编号(1、2或3),ll,rr,xx
输出格式:
每次进行3操作,输出一行表示答案
记得膜模1000000007
输入输出样例
5 5 19844 14611 26475 4488 6967 2 1 3 15627 2 1 2 30113 2 3 5 14686 2 5 5 32623 3 1 2 8
466266421
说明
kk表示询问的幂的大小,也就是操作3对应的xx。
对于20%的数据,满足n,mleq 1000n,m≤1000
对于另外20%的数据,满足kleq 1k≤1
对于另外20%的数据,满足kleq 2k≤2
对于另外20%的数据,满足n,mleq 50000n,m≤50000
对于100%的数据,满足n,mleq 100000,0leq k leq 10n,m≤100000,0≤k≤10
操作1,2对应的xle 10^9+7x≤109+7
===========
解:线段树;
维护p[i]即为i次方;
难在ch_add函数,用二项式定理:
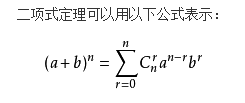
好好看ch_add函数;

#include<cstdio> #include<cstring> #define ll long long const ll N=100010; const ll mod=1e9+7; struct node { ll l,r; ll la_add,la_set,p[12]; }e[N<<3]; ll c[12][12]; #define ls ro<<1 #define rs ro<<1|1 inline void pushup(ll ro) { for(ll i=0;i<=10;i++) e[ro].p[i]=(e[ls].p[i]+e[rs].p[i])%mod; } void build(ll ro,ll l,ll r) { e[ro].l=l,e[ro].r=r;e[ro].la_set=-1,e[ro].la_add=0; if(l==r) { ll x; scanf("%lld",&x); e[ro].p[0]=1; for(ll i=1;i<=10;i++) e[ro].p[i]=e[ro].p[i-1]*x%mod; return; } ll mid=(l+r)>>1; build(ls,l,mid);build(rs,mid+1,r); pushup(ro); } inline void ch_add(ll ro,ll x) { for(int i=10;i>=0;i--) { ll res=1,t=0; for(int j=i;j>=0;j--) { t=(t+e[ro].p[j]*c[i][j]%mod*res)%mod; res=res*x%mod; } e[ro].p[i]=t; } e[ro].la_add=(e[ro].la_add+x)%mod; } inline void ch_set(ll ro,ll x) { ll res=1; for(ll i=0;i<=10;i++) { e[ro].p[i]=res*(e[ro].r-e[ro].l+1)%mod; res=res*x%mod; } e[ro].la_add=0; e[ro].la_set=x; } inline void down(ll ro) { if(e[ro].la_set!=-1) { ch_set(ls,e[ro].la_set); ch_set(rs,e[ro].la_set); e[ro].la_set=-1; } if(e[ro].la_add) { ch_add(ls,e[ro].la_add); ch_add(rs,e[ro].la_add); e[ro].la_add=0; } } void add(ll ro,ll l,ll r,ll x) { down(ro); if(l<=e[ro].l&&e[ro].r<=r) { ch_add(ro,x); return; } ll mid=(e[ro].l+e[ro].r)>>1; if(l<=mid) add(ls,l,r,x); if(r>mid) add(rs,l,r,x); pushup(ro); } void set(ll ro,ll l,ll r,ll x) { down(ro); if(l<=e[ro].l&&e[ro].r<=r) { ch_set(ro,x); return; } ll mid=(e[ro].l+e[ro].r)>>1; if(l<=mid) set(ls,l,r,x); if(r>mid) set(rs,l,r,x); pushup(ro); } ll query(ll ro,ll l,ll r,ll x) { down(ro); if(l<=e[ro].l&&e[ro].r<=r) return e[ro].p[x]; ll mid=(e[ro].l+e[ro].r)>>1; ll ans=0; if(l<=mid) ans=(ans+query(ls,l,r,x))%mod; if(mid<r) ans=(ans+query(rs,l,r,x))%mod; return ans; } int main() { ll n,m; scanf("%lld %lld",&n,&m); build(1,1,n); // for(ll i=1;i<=20;i++) // { // printf("std:: %lld %lld %lld %lld ",e[i].l,e[i].r,e[i].la_add,e[i].la_set); // for(ll j=0;j<=10;j++) printf("%lld ",e[i].p[j]); // printf(" "); // } c[0][0]=1; for(ll i=1;i<=10;i++) { c[i][0]=1; for(ll j=1;j<=i;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; } // for(int i=0;i<=10;i++) // { // for(int j=0;j<=i;j++) // printf("%lld ",c[i][j]); // printf(" "); // } ll dp,l,r,x; for(ll i=1;i<=m;i++) { scanf("%lld %lld %lld %lld",&dp,&l,&r,&x); if(dp==1) add(1,l,r,x); else if(dp==2) set(1,l,r,x); else printf("%lld ",query(1,l,r,x)); } return 0; }
============
