Misha and Forest
Time Limit:1000MS Memory Limit:262144KB 64bit IO Format:%I64d & %I64uDescription
Let's define a forest as a non-directed acyclic graph (also without loops and parallel edges). One day Misha played with the forest consisting of n vertices. For each vertex v from 0 to n - 1 he wrote down two integers, degreev and sv, were the first integer is the number of vertices adjacent to vertex v, and the second integer is the XOR sum of the numbers of vertices adjacent to v (if there were no adjacent vertices, he wrote down 0).
Next day Misha couldn't remember what graph he initially had. Misha has values degreev and sv left, though. Help him find the number of edges and the edges of the initial graph. It is guaranteed that there exists a forest that corresponds to the numbers written by Misha.
Input
The first line contains integer n (1 ≤ n ≤ 216), the number of vertices in the graph.
The i-th of the next lines contains numbers degreei and si (0 ≤ degreei ≤ n - 1, 0 ≤ si < 216), separated by a space.
Output
In the first line print number m, the number of edges of the graph.
Next print m lines, each containing two distinct numbers, a and b (0 ≤ a ≤ n - 1, 0 ≤ b ≤ n - 1), corresponding to edge (a, b).
Edges can be printed in any order; vertices of the edge can also be printed in any order.
Input
3
2 3
1 0
1 0
Output
2
1 0
2 0
Input
2
1 1
1 0
Output
1
0 1
Hint
The XOR sum of numbers is the result of bitwise adding numbers modulo 2. This operation exists in many modern programming languages. For example, in languages C++, Java and Python it is represented as "^", and in Pascal — as "xor".
下面是大神博客里面的东西,代码注释是我加的,希望可以帮助大家理解
【题目意思】有 n 个点,编号为 0 ~ n-1。给出 n 个点的度数(即有多少个点跟它有边相连)以及跟它相连的点的编号的异或结果。最后需要输出整幅图的所有边的情况。
这道题确实是一道很好的题目!!!!它说拓扑排序的变形,需要队列的运用,还有就是异或计算的性质!!!(非一般厉害)
由于是无向无环的简单图,换言之就是一棵树啦^_^。那么它就肯定有叶子结点,叶子节点的度数为1,此时它相邻点的异或结果实际上就是所求点的编号了。然后把跟叶子节点相邻的点的度数-1,代表把叶子节点去除,此时异或结果是有变的。需要用本来的异或结果跟该叶子节点再异或一次,就得出除了这个叶子节点外其他点的异或值了。举个例子吧,假如有一幅图是这样的。
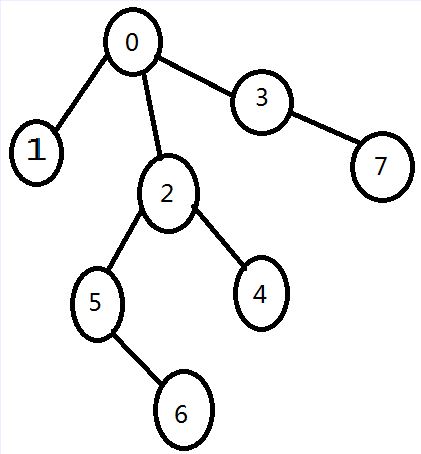
0 的相邻点有1、 2、 3,异或出来的结果是0,它的度数是3.那么当处理0-1这条边时,容易知道去除1这个点后,只有2和3异或了:10 ^ 11 = 1,刚好等于 1 ^ 2 ^ 3 ^ 1 (01 ^ 10 ^ 11 ^ 01)。异或的一个性质就是a^b^c^a = b ^ c。是不是很神奇呢~~~~当然我们总是处理那些度数为1的点,把这些点放入队列里面,依次处理。
个人觉得代码中的degree[i]理解为与i相连的点的个数比较恰当
AC代码:
1 //异或(^) 0^0=1^1=0 相同为0,1^0=0^1=1不同为1 2 #include <iostream> 3 #include <cstdio> 4 #include <cstdlib> 5 #include <queue> 6 using namespace std; 7 8 #define f first//子节点 9 #define s second//父节点 10 11 const int maxn = (1<<16) + 5;//2的16次方+5 12 int degree[maxn], XOR_sum[maxn]; 13 14 int main() 15 { 16 int n; 17 while (scanf("%d", &n) != EOF) 18 { 19 queue<int> q; 20 pair<int, int> ans[maxn]; 21 for (int i = 0; i < n; i++) 22 { 23 scanf("%d%d", °ree[i], &XOR_sum[i]); 24 if (degree[i] == 1)//叶子相连的点只有一个,是叶子就进队 25 q.push(i); 26 } 27 int cnt = 0;//记录边的个数 28 while (!q.empty()) 29 { 30 int from = q.front();//叶子 31 q.pop(); 32 if (degree[from] == 1)// 这句判断很重要,因为有可能degree[]--过程中使得变为0 33 {//处理的是叶子 34 int to = XOR_sum[from];//叶子结点的异或和是父节点 35 ans[cnt].f = from;//from子节点 36 ans[cnt++].s = to;//to是父节点 37 degree[to]--;//父节点to相邻点的个数-1 38 XOR_sum[to] ^= from;//把与to相连的子节点from删除,异或性质a^b^c^a = b^c 39 if (degree[to] == 1) 40 q.push(to); 41 } 42 } 43 printf("%d ", cnt); 44 for (int i = 0; i < cnt; i++) 45 printf("%d %d ", ans[i].f, ans[i].s); 46 } 47 return 0; 48 }