适用条件:
给定一个规模较大的数组,其中元素变更频繁,随时对数组中所有数的求和。
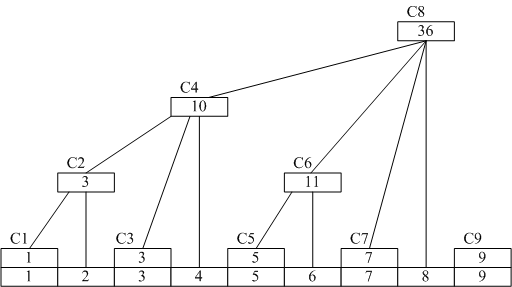
图中底层为给定数组a,上层为辅助求解的树状数组c,二者之间的关系为 :
当c的下标i为奇数时,c[i] = a[i];
当c的下标i为偶数时,取决于i的因子中最大的一个“2的整数次幂”是多少,如6的因子中为2,则c[6] = a[5] + a[6];
求解树状数组:
根据以上分析可写出关系式:c[i] = a[i-2^k+1] + …… + a[i]; 那么难点就是求解i所对应的2^k怎么求?
(其中k为i的二进制表示中末尾0的个数,根据右移规律可知,2^k即i的因子中最大的一个“2的整数次幂”)
int lowbit(int x) { return x & (-x); }
求出c数组后,下面就可对整个数组进行求和了。
给定数组求和:
若求数组前6个数和,依据树状图可知sum = c[6] + c[4];
int Sum(int n) { int sum = 0; while(n > 0) { sum += c[n]; n -= lowbit(n); // 将n的二进制表示最后一个1的位置减一 } return sum; }
修改数组元素:
若对a[5]加上数x,则c[5], c[6], c[8]都要依次调整;
void Change(int i, int x) { while(i <= n) { c[i] += x; i += lowbit(i); // 将n的二进制表示最后一个1的位置加一 } }