前置知识
- 最近公共祖先(LCA),树形DP,DFS序,链式前向星存图,线段树
功能
对一棵树进行剖分,将其分成几条链,将树形变为线性,减少处理的难度
需要处理的问题有
- 将树从(x)到(y)结点最短路径上所有节点的值都加上(z)
- 求树从(x)到(y)结点最短路径上所有节点的值之和
- 将以(x)为根节点的子树内所有节点值都加上(z)
- 求以(x)为根节点的子树内所有节点值之和
定义及概念
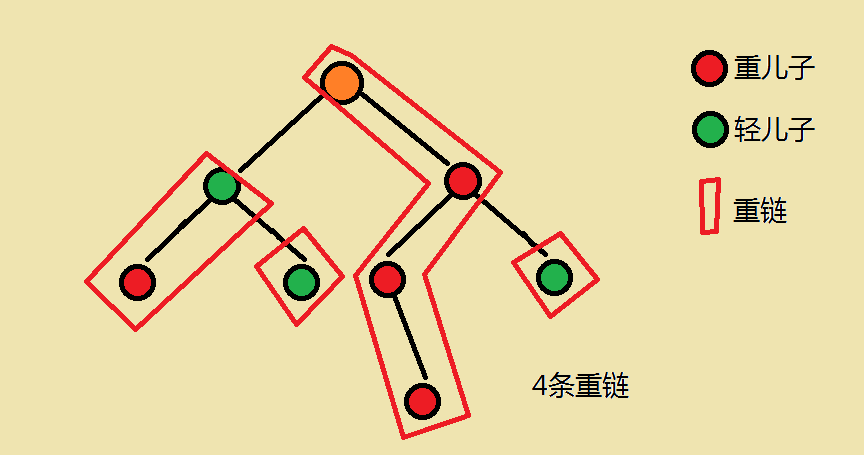
- 重儿子:对于每一个非叶子节点,他的儿子中以那个儿子为根的子树的节点数最大的儿子,为该点的重儿子
- 轻儿子:对于每个非叶子节点,他的儿子中不是重儿子的剩下的所有儿子就是轻儿子
- 叶子节点没有重儿子也没有轻儿子,因为他根本没有儿子(QAQ)
- 重边:一个父亲连接他的重儿子的边称为重边
- 轻边:重边剩下的就是轻边
- 重链:相邻的重边连起来的连接一条重儿子的链称为重链
- 对于叶子节点,如果他是轻儿子,那么有一条以他自己为起点的长度为1的链
- 每一条重链以其轻儿子为起点
步骤
(DFS1)
功能
- 标记每个点的深度
- 标记每个点的父亲
- 标记每个非叶子的子树大小(包括他自己)
- 标记每个非叶子节点的重儿子的编号
代码实现
void dfs1(int x,int f,int deep)//x当前节点,f父亲,deep深度
{
dep[x]=deep;//标记深度
fa[x]=f;//标记每个点的父亲
siz[x]=1;//标记每个非叶子节点的子树的大小
int maxson=-1;//记录重儿子的儿子数量
for(int i=head[x];i;i=e[i].last)
{
int y=e[i].to;
if(y==f) continue;//如果是父亲那么就继续去找下一个
dfs1(y,x,deep+1);
siz[x]+=siz[y];//加上子树的节点数量
if(siz[y]>maxson)
{
son[x]=y;
maxson=siz[y];//如果该子节点更大,那么就标记他的每个非叶子节点的
//重儿子的编号
}
}
}
(DFS2)
功能
- 标记每一个点的新编号(在线段树里面的)
- 给每个点的新编号赋上这个点的初始值
- 处理好每个点所在的链的顶端
- 处理每条链
代码实现(先处理重儿子,再处理轻儿子)
void dfs2(int x,int topf)//x为当前的节点,topf为当前链上最顶端的节点
{
id[x]=++cnt;//标记每个点的新编号
wt[cnt]=w[x];//把每个点的初始值都赋到新的编号上来
top[x]=topf;//标记这个点所在的链的顶端
if(!son[x]) return;//如果没有重儿子(儿子),那么就返回
dfs2(son[x],topf);//先处理重儿子,在处理轻儿子,递归处理
for(int i=head[x];i;i=e[i].last)
{
int y=e[i].to;
if(y==fa[x]||y==son[x])continue;
//如果遍历到父亲结点或者是重儿子,那么就继续搜索
dfs2(y,y);
//每一个轻儿子都有一条从自己开始的链
}
}
处理问题
- 先标上新的编号
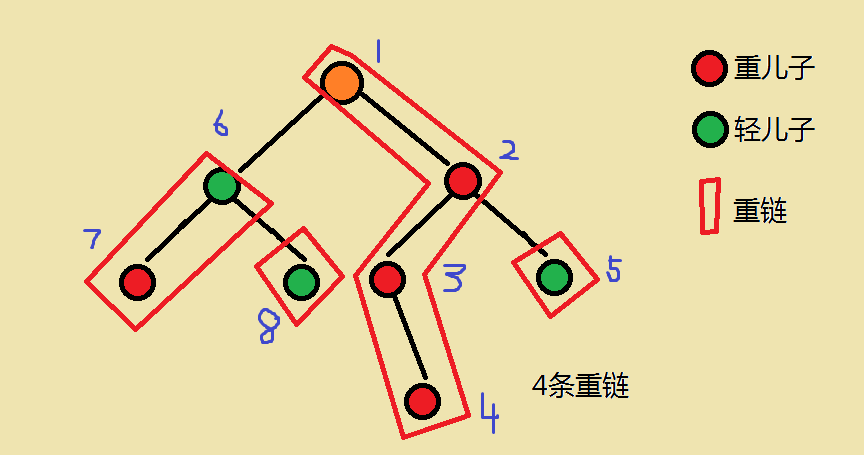
因为顺序是按照先重儿子,再轻儿子来处理的,所以每一条重链的新编号是连续的
因为是用的(DFS)所以每一个子树的新编号也是连续的
- 首先,当我们要处理任意两点间的路径时:
设我们所在练的顶端深度更深的那个点为(x)点- (ans)加上(x)点到(x)所在链的顶端这一段区间的点权和
- 把(x)跳到(x)所在的链顶端的那个点的上面的那个点
- 不断地执行这两个操作,知道这两个点处在一条链上面,然后此时在加上这两个点之间的区间和
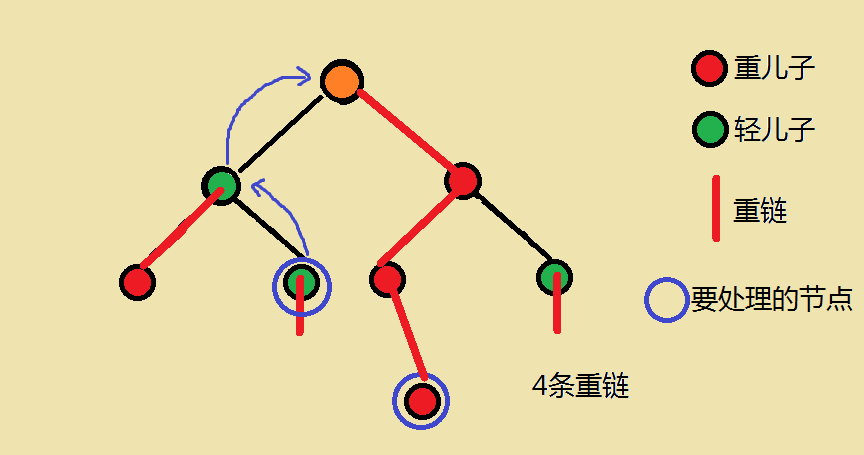
在这个时候我们注意到,我们所要处理的所有的区间都是连续的编号(新编号),那么我们可以用线段树处理连续编号区间和,每次查询时间复杂度为(O(log^2n))
int qRange(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])//把x改在所在链更深的点
swap(x,y);
res=0;
query(1,1,n,id[top[x]],id[x]);//ans加上x点到所在链顶端的这一区间的点权和
ans+=res;
ans%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
res=0;
query(1,1,n,id[x],id[y]);
ans+=res;
return ans%mod;
}
处理一点及其子树的点权和
记录每一个非叶子节点的子树的大小,并且每一个子树的新编号都是连续的,于是就直接线段树区间查询即可时间复杂度为(O(log n))
int qson(int x)
{
res=0;
query(1,1,n,id[x],id[x]+siz[x]-1);//子树的右端点为id[x]+siz[x]-1,可以手推一下
return res;
}
区间修改
void updson(int x,int k)
{
update(1,1,n,id[x],id[x]+siz[x]-1,k);
}
void updRange(int x,int y,int k)//区间修改
{
k%=mod;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])//让x的深度更深
swap(x,y);
update(1,1,n,id[top[x]],id[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
update(1,1,n,id[x],id[y],k);
}
完整代码(200行高能)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<cmath>
#include<algorithm>
using namespace std;
#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define len (r-l+1)
const int N=2e5+10;
struct node{
int last;
int to;
}e[N];
int head[N];
int n,m,r,mod;
int e_cnt,w[N],wt[N];
int a[N<<2],laz[N<<2];
//线段树数组,懒惰标记
int son[N],id[N],fa[N],cnt,dep[N],siz[N],top[N];
//重儿子编号,新编号,父亲结点,dfs序,深度,子树的大小,当前链的顶端结点
int res=0;
void add(int from,int to)
{
e[++e_cnt].last=head[from];
e[e_cnt].to=to;
head[from]=e_cnt;
}
//------------------------------------------------线段树
void pushdown(int rt,int lenn)
{
laz[rt<<1]+=laz[rt];
laz[rt<<1|1]+=laz[rt];
a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
a[rt<<1|1]+=laz[rt]*(lenn>>1);
a[rt<<1]%=mod;
a[rt<<1|1]%=mod;
laz[rt]=0;
}
void build(int rt,int l,int r)
{
if(l==r)
{
a[rt]=wt[l];//赋值点权值
if(a[rt]>mod) a[rt]%=mod;
return;
}
build(lson);
build(rson);
a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
}
void query(int rt,int l,int r,int L,int R)
{
if(L<=l&&r<=R)
{
res+=a[rt];
res%=mod;
return;
}
else
{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) query(lson,L,R);
if(R>mid) query(rson,L,R);
}
}
void update(int rt,int l,int r,int L,int R,int k)
//当前节点,当前区间的左,右,要修改的区间左,右,修改值
{
if(L<=l&&r<=R)
{
laz[rt]+=k;
a[rt]+=k*len;
}
else
{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) update(lson,L,R,k);
if(R>mid) update(rson,L,R,k);
a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
}
}
//------------------------------------------------树链剖分
int qRange(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])//把x改在所在链更深的点
swap(x,y);
res=0;
query(1,1,n,id[top[x]],id[x]);//ans加上x点到所在链顶端的这一区间的点权和
ans+=res;
ans%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
res=0;
query(1,1,n,id[x],id[y]);
ans+=res;
return ans%mod;
}
void updRange(int x,int y,int k)//区间修改
{
k%=mod;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])//让x的深度更深
swap(x,y);
update(1,1,n,id[top[x]],id[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
update(1,1,n,id[x],id[y],k);
}
int qson(int x)
{
res=0;
query(1,1,n,id[x],id[x]+siz[x]-1);
return res;
}
void updson(int x,int k)
{
update(1,1,n,id[x],id[x]+siz[x]-1,k);
}
void dfs1(int x,int f,int deep)//x当前节点,f父亲,deep深度
{
dep[x]=deep;//标记深度
fa[x]=f;//标记每个点的父亲
siz[x]=1;//标记每个非叶子节点的子树的大小
int maxson=-1;//记录重儿子的儿子数量
for(int i=head[x];i;i=e[i].last)
{
int y=e[i].to;
if(y==f) continue;//如果是父亲那么就继续去找下一个
dfs1(y,x,deep+1);
siz[x]+=siz[y];//加上子树的节点数量
if(siz[y]>maxson)
{
son[x]=y;
maxson=siz[y];//如果该子节点更大,那么就标记他的每个非叶子节点的
//重儿子的编号
}
}
}
void dfs2(int x,int topf)//x为当前的节点,topf为当前链上最顶端的节点
{
id[x]=++cnt;//标记每个点的新编号
wt[cnt]=w[x];//把每个点的初始值都赋到新的编号上来
top[x]=topf;//标记这个点所在的链的顶端
if(!son[x]) return;//如果没有重儿子(儿子),那么就返回
dfs2(son[x],topf);//先处理重儿子,在处理轻儿子,递归处理
for(int i=head[x];i;i=e[i].last)
{
int y=e[i].to;
if(y==fa[x]||y==son[x])continue;
//如果遍历到父亲结点或者是重儿子,那么就继续搜索
dfs2(y,y);
//每一个轻儿子都有一条从自己开始的链
}
}
int main()
{
cin>>n>>m>>r>>mod;
for(int i=1;i<=n;i++)
cin>>w[i];//节点的初始权值
for(int i=1;i<n;i++)
{
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
dfs1(r,0,1);
dfs2(r,r);
build(1,1,n);
while(m--)
{
int k,x,y,z;
cin>>k;
if(k==1)
{
cin>>x>>y>>z;
updRange(x,y,z);
}
else if(k==2)
{
cin>>x>>y;
cout<<qRange(x,y)<<endl;
}
else if(k==3)
{
cin>>x>>y;
updson(x,y);
}
else
{
cin>>x;
cout<<qson(x)<<endl;
}
}
return 0;
}