codeforces #323 div 2 C. GCD Table (暴力？)

C. GCD Table

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The GCD table G of size n × n for an array of positive integers a of length n is defined by formula

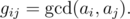
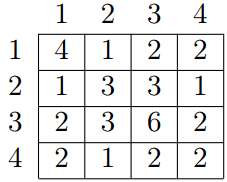
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both x and y, it is denoted as 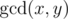. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:

Given all the numbers of the GCD table G, restore array a.

Input

The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.

All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.

Output

In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.

Sample test(s)

input

4
2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2

output

4 3 6 2

input

1
42

output

42 

input

2
1 1 1 1

output

1 1 

被hack了．．sad．
首先可以发现一些结论
１：对角线上的数就是原序列
２：table关于对角线对称
３：出现奇数次数一定是原序列中的数（这个结论并没有用到，不过这是首先能想到的，用到用不到再说）
４：gcd(a,b)<=min(a,b)；

然后我之前的做法是用一个map统计出现的次数
然后遍历map，先把出现奇数的挑出来.算作一个答案．并把次数-1
这样所有的都是出现１

/*************************************************************************
    > File Name: code/#323/CC.cpp
    > Author: 111qqz
    > Email: rkz2013@126.com 
    > Created Time: 2015年10月04日 星期日 14时51分08秒
 ************************************************************************/

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
#include<cctype>
                 
#define yn hez111qqz
#define j1 cute111qqz
#define ms(a,x) memset(a,x,sizeof(a))
using namespace std;
const int dx4[4]={1,0,0,-1};
const int dy4[4]={0,-1,1,0};
typedef long long LL;
typedef double DB;
const int inf = 0x3f3f3f3f;
const int N=5E2+7;
int a[N*N];
int n;
map<int,int>mp;
vector<int> ans;
int gcd(int a,int b) { return b==0?a:gcd(b,a%b);}
int main()
{
  #ifndef  ONLINE_JUDGE 
   freopen("in.txt","r",stdin);
  #endif
   mp.clear();
   scanf("%d",&n);
   for ( int i = 0 ; i < n*n ; i++)
    {
    scanf("%d",&a[i]);
    mp[a[i]]++;
    }
    sort(a,a+n*n);

    for ( int i = n*n-1 ;i>=0 ; i--)
    {
    if (!mp[a[i]]) continue;
    mp[a[i]]--;
    for ( int j = 0 ; j< ans.size() ; j++)
    {
        int tmp = gcd(a[i],ans[j]);
        mp[tmp]--;
        mp[tmp]--;
    }
    ans.push_back(a[i]);
    }
    for ( int i = 0 ; i < n-1 ; i++)
    printf("%d ",ans[i]);
    printf("%d",ans[n-1]);

  
   
 #ifndef ONLINE_JUDGE  
  fclose(stdin);
  #endif
    return 0;
}

偶数次
然后我从大往小加，直到有n个为止（算上之前的奇数次的）
错了是因为我想当然得以为...n个数的gcd table 中...对于任意一对gcd(a,b)（a!=b）一定小于等于所有的原始数列的数．．．
这显然不对...因为第四点的小于等于关系只是针对某对数的局部结论，而没办法推到整体...想当然了．好傻逼啊．．．

正确的做法其实很接近了...
由于第四个可以知道...最大的数一定是原始数列中的数...
我们可以从已经确定为原始数列的数来排除掉答案．
由于对称性...将a[i]排序后从大到小枚举...每个新出现的数和已经确定为原始数列的数为产生一对相等的gcd．．．减掉就可以了．
具体见代码：