codeforces #319 div 2 E C. Points on Plane (分块)

E. Points on Plane

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

On a plane are n points (xi, yi) with integer coordinates between 0 and 106. The distance between the two points with numbers a and b is said to be the following value: 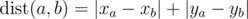 (the distance calculated by such formula is called Manhattan distance).

We call a hamiltonian path to be some permutation pi of numbers from 1 to n. We say that the length of this path is value .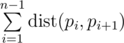

Find some hamiltonian path with a length of no more than 25 × 108. Note that you do not have to minimize the path length.

Input

The first line contains integer n (1 ≤ n ≤ 106).

The i + 1-th line contains the coordinates of the i-th point: xi and yi (0 ≤ xi, yi ≤ 106).

It is guaranteed that no two points coincide.

Output

Print the permutation of numbers pi from 1 to n — the sought Hamiltonian path. The permutation must meet the inequality .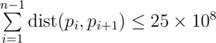

If there are multiple possible answers, print any of them.

It is guaranteed that the answer exists.

Sample test(s)

input

5
0 7
8 10
3 4
5 0
9 12

output

4 3 1 2 5 

Note

In the sample test the total distance is:

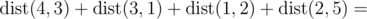
(|5 - 3| + |0 - 4|) + (|3 - 0| + |4 - 7|) + (|0 - 8| + |7 - 10|) + (|8 - 9| + |10 - 12|) = 2 + 4 + 3 + 3 + 8 + 3 + 1 + 2 = 26

初识分快.

引一段题解：

Let's split rectangle 106 × 106 by vertical lines into 1000 rectangles 103 × 106. Let's number them from left to right. We're going to pass through points rectangle by rectangle. Inside the rectangle we're going to pass the points in increasing order of y-coordinate if the number of rectangle is even and in decreasing if it's odd.

Let's calculate the maximum length of such a way. The coordinates are independent. By y-coordinate we're passing 1000 rectangles from0 to 106, 109 in total. By x-coordinate we're spending 1000 to get to the next point of current rectangle and 2000 to get to next rectangle. That means, 2 * 109 + 2000000 in total, which perfectly fits.

The complexity is O(n * log(n))

 并不会做，看了题解写的，感觉好神奇...

然后加深了sort的cmp函数的理解．．．

原来还可以这么写．

有点开心，因为觉得解法有点美．

/*************************************************************************
    > File Name: code/cf/#319/E.cpp
    > Author: 111qqz
    > Email: rkz2013@126.com 
    > Created Time: 2015年09月18日 星期五 20时55分10秒
 ************************************************************************/

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
#include<cctype>
#define y1 hust111qqz
#define yn hez111qqz
#define j1 cute111qqz
#define ms(a,x) memset(a,x,sizeof(a))
#define lr dying111qqz
using namespace std;
#define For(i, n) for (int i=0;i<int(n);++i)  
typedef long long LL;
typedef double DB;
const int inf = 0x3f3f3f3f;
const int N=1E6+7;
int n;
int id[N],x[N],y[N];

bool cmp(int a,int b) //id[a] 和id[b]的大小比较定义
{
    if (x[a]<x[b]) return true;
    if (x[a]>x[b]) return  false;
    if (x[a]%2==1) return y[a]<y[b];
    else  return y[a]>y[b];                   //sort的cmp函数原来还可以这么写，长见识了．
    
}
int main()
{
  #ifndef  ONLINE_JUDGE 
    freopen("in.txt","r",stdin);  
  #endif
    scanf("%d",&n);
    for ( int i = 0 ; i < n ; i++)
    {
    scanf("%d %d",&x[i],&y[i]);
    x[i] /=1000;
    y[i] /=1000;
    id[i] = i;
    }
    sort(id,id+n,cmp);
    for ( int i = 0 ; i < n ; i++)
    {
    printf("%d ",id[i]+1);
    }
    

  
  
 #ifndef ONLINE_JUDGE  
  fclose(stdin);
  #endif
    return 0;
}