卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学中一个常出现在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名,其前几项为 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
力扣96
给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种?
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
 

一种解释
首先注意,dp [k]表示从1 ... k构建的BST树的数量;
那么假设我们有前4棵树的数量:dp [1] = 1,dp [2] = 2,dp [3] = 5,dp [4] = 14,我们如何得到dp [5]这四个数字是这里的核心问题。
基本的过程是:构建一棵树,我们需要选择一个根节点,然后我们需要知道在该节点下可以保留多少个可能的左子树和右子树,最后将它们相乘。
构建一个包含{1,2,3,4,5}的树。首先我们选择1作为根,对于左边的子树,没有;对于正确的子树,我们需要计算从{2,3,4,5}构建的树有多少棵,显然它与{1,2,3,4}的数相同。因此,根据“1”选取的树的总数为dp [0] * dp [4] = 14(假设dp [0] = 1)。同样,根2具有dp [1] * dp [3] = 5个树。根3具有dp [2] * dp [2] = 4,根4具有dp [3] * dp [1] = 5并且根5具有dp [0] * dp [4] = 14。完成。
一种解释
二叉搜索树的数量可视化为
二叉搜索树的数量=
(根可以选择的路数)*
(左二叉搜索子树的数量)*
(右二叉搜索子树的数量)
现在,由于在BST中存在“n”个节点并且,所以对于n个元素,BST的数量由C(n)表示。
我们可以递归地查找BST的数量:
选择1作为根,左子树上没有元素。 右子树上有n-1个元素。
选择2作为根,左子树上的1个元素。 右子树上的n-2个元素。
选择3作为根,左侧子树选择2个元素。 右子树上的n-3个元素。
同样,对于第i个元素作为根,左边的i-1元素和右边的n-i。
这些子树也是BST,所以我们可以这样写:
C(n) = C(0)C(n-1) + C(1)C(n-2) + .....+ C(i-1)C(n-i)..... + C(n-1)C(0)
C(0)= 1,因为只有一种方法可以生成0节点的BST。 C(1)= 1,因为有一个方法可以使1个节点的BST生成。
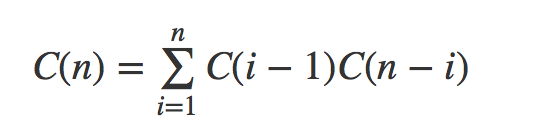 

代码
public int numTrees(int n) {
int [] dp = new int[n+1];
dp[0]= 1;
dp[1] = 1;
for(int level = 2; level <=n; level++)
for(int root = 1; root<=level; root++)
dp[level] += dp[level-root]*dp[root-1];
return dp[n];
}