这些问题归为哈希表,倒不一定都是要建哈希表来做,有的题目可以用定长的数组起到哈希表的作用。
而且很多题有其他更好一些的方法。
数组中的问题
两数之和 1题(easy):
给定一个整数数组和一个目标值,找出数组中和为目标值的两个数。
你可以假设每个输入只对应一种答案,且同样的元素不能被重复利用。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
分析:
暴力方法时间复杂度要O( n^2 ),使用哈希表可以降低到O(n);而且只需一趟扫描存值就可以。
代码:
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement)) { //存值之前先在哈希表中查此元素的“配对”元素是否在其中
return new int[] { map.get(complement), i };
}
map.put(nums[i], i);//因为在后续查找中要查的是数组中存的值,所以key存num[i]
}
throw new IllegalArgumentException("No two sum solution");//抛异常
}
存在重复元素 217题(easy):
给定一个整数数组,判断是否存在重复元素。
如果任何值在数组中出现至少两次,函数返回 true。如果数组中每个元素都不相同,则返回 false。
分析:
最简单的题目了,很多种方法:
1.暴力法 两个for循环 O(n^2) O(1)
2.排序法 先排序 看临近的是否相等 O(NlogN)O(1)
3.哈希表法 一个个往哈希表里存 O(n) O(n)
代码:
public boolean containsDuplicate(int[] nums) {
Set<Integer> set = new HashSet<>(nums.length);
for (int x: nums) {
if (set.contains(x)) return true;
set.add(x);
}
return false;
}
存在重复元素II 219题:
给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] = nums [j],并且 i 和 j 的差的绝对值最大为 k。
示例:
输入: nums = [1,2,3,1], k = 3
输出: true
输入: nums = [1,2,3,1,2,3], k = 2
输出: false
分析:
这题最开始想法是用hashmap,类似I只是加个下标多个判断,但是不够巧妙。高票答案是Buckets方法,哈希表中维持一个容量为k+1个元素的“滑动窗”,相当于在限定窗长度的条件之上找重复,只用hashset就够了。
代码:
public boolean containsNearbyDuplicate(int[] nums, int k) {
Set<Integer> set = new HashSet<Integer>();
for(int i = 0; i < nums.length; i++){
if(i > k) set.remove(nums[i-k-1]); //把最前面一个元素删掉
if(!set.add(nums[i])) return true; //add的同时就判断重复了,重复就return
}
return false;
}
有效的数独 36题:
判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

数独部分空格内已填入了数字,空白格用 '.' 表示。
示例:
输入:
[
["8","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。
但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
说明:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
给定数独序列只包含数字 1-9 和字符 '.' 。
给定数独永远是 9x9 形式的。
分析:
这题是基于一个矩阵的问题,简单的思路就是将每行,每列,每块分别建一个hashset来判断重复元素(一共建27个)。关键在于怎样巧妙地实现在一个双重for循环当中,怎么样根据二维数组的的两个坐标,将值存到对应的27个哈希表中。
二维数组中的每个值都要遍历到,而且每个值都要存到对应的行列块哈希表中。
下面的代码使用%和/两个运算符来帮助解决矩阵遍历问题;
对于块遍历,它使用如下方式:
0,0,0,1,0,2,<--- 3个水平step,然后是1个垂直step到下一个级别。
1,0,1,1,1,2,<--- 3个水平step,然后是1个垂直step到下一个级别。
2,0,2,1,2,2,<--- 3个水平step。
依次类推....
但是,j的迭代来自于0-9
但我们需要在3个水平step后停止,并垂直向下1个step
使用%来进行水平step,因为j%3 对于每一个j增加1,结果也增加1:0%3 = 0 , 1%3 = 1, 2%3 = 2
增加3次以后重置。所以这包括每个块的水平遍历三次
使用/来进行垂直step 因为/ ,每三个j增加1:0/3 = 0; 1/3 = 0; 2/3 =0; 3/3 = 1
所以到目前为止,对于一个给定的块,可以用j来遍历整个的块。
但是因为j只是0-9,所以只会停留在第一个块,如果要增加块,就要用到i了。
水平step到下一个块,用%,注意这里要乘3了,即ColIndex = 3 * i%3,使得下一个块在3列之后,即0,0第一个块的开始,第二个块是0,3(不是0,1)。同样,要垂直移动到下一个块,要使用/并乘以3。
代码:
public boolean isValidSudoku(char[][] board) {
for(int i = 0; i<9; i++){
HashSet<Character> rows = new HashSet<Character>();
HashSet<Character> columns = new HashSet<Character>();
HashSet<Character> cube = new HashSet<Character>();
for (int j = 0; j < 9;j++){
if(board[i][j]!='.' && !rows.add(board[i][j])) //存行i的set
return false;
if(board[j][i]!='.' && !columns.add(board[j][i]))//存列i的set
return false;
int RowIndex = 3*(i/3);
int ColIndex = 3*(i%3);
if(board[RowIndex + j/3][ColIndex + j%3]!='.' && !cube.add(board[RowIndex + j/3][ColIndex + j%3])) //存块i的set
return false;
}
}
return true;
}
字符串中的问题
无重复字符的最长子串 3题:
给定一个字符串,找出不含有重复字符的最长子串的长度。
示例:
给定 "abcabcbb" ,没有重复字符的最长子串是 "abc" ,那么长度就是3。
给定 "bbbbb" ,最长的子串就是 "b" ,长度是1。
给定 "pwwkew" ,最长子串是 "wke" ,长度是3。请注意答案必须是一个子串,"pwke" 是序列而不是子串。
分析:
无重复问题使用哈希表是一个方法,要注意选用hashset还是hashmap;这道题技巧在于使用hashmap同时存值和下标;在检测重复的能够定位到重复的值的那个下标。使用双指针标记子串起止,试图扩展子串。
代码:
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
Map<Character, Integer> map = new HashMap<>(); // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
if (map.containsKey(s.charAt(j))) {
i = Math.max(map.get(s.charAt(j))+1, i);//i不必每次只增加1,而是一步到位,加到与当前元素重复的旧索引处+1。
//i不能回退,更新时取最大,例如:“caac“
}
map.put(s.charAt(j), j);
ans = Math.max(ans, j - i+1 ); //更新最大长度ans
}
return ans;
}
有效的字母异位词 242题(easy):
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的一个字母异位词。
说明:
你可以假设字符串只包含小写字母。
进阶:
如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
示例:
输入: s = "anagram", t = "nagaram"
输出: true
输入: s = "rat", t = "car"
输出: false
分析:
如果只考虑只包含小写字母,就是建一个长度为26的数组,数组中的每个位置相当于对应字母的计数器,最后检查数组并返回。
也还有其他方法:
1.排序法 String转为CharArray再排序
2.哈希表法 用hashmap存,value存出现的次数
3.素数法(不好,溢出) 每个字母用不同的素数表示,乘起来,结果一样说明是字母异位
代码:
public boolean isAnagram(String s, String t) {
if (s.length()!=t.length()) return false;
char[] a=new char[26];
for (int i=0;i<s.length();i++){
a[s.charAt(i)-'a']++;
a[t.charAt(i)-'a']--;
}
for (int j=0;j<a.length;j++){
if (a[j]!=0) return false;
}
return true;
}
字母异位词分组 49题:
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。
示例:
输入: ["eat", "tea", "tan", "ate", "nat", "bat"],
输出:
[
["ate","eat","tea"],
["nat","tan"],
["bat"]
]
说明:
所有输入均为小写字母。
不考虑答案输出的顺序。
分析:
这题的常规想法肯定就是使用一个长度为26的数组来存一个字符串中相应位置上的字母是有还是无,如果两个字符串是异位词,那么纪录后的两个数组一定是一样的。但是这么做还是不好,复杂度最高O(N^2)。
这题的技巧在于sort。一个字符串转为字符数组后可以进行sort操作。这样,如果两个字符串是异位词,sort后是一样的。使用hashmap,key是sort后的字符串,value是List
代码:
public List<List<String>> groupAnagrams(String[] strs) {
if (strs == null || strs.length == 0) return new ArrayList<List<String>>();
Map<String, List<String>> map = new HashMap<String, List<String>>();
for (String s : strs) {
char[] ca = s.toCharArray();
Arrays.sort(ca);
String keyStr = String.valueOf(ca);
if (!map.containsKey(keyStr)) map.put(keyStr, new ArrayList<String>());
map.get(keyStr).add(s);
}
return new ArrayList<List<String>>(map.values());//这一步ArrayList的构造方法,注意map.values()返回的是map中所有值的一个视图。
}
重复的DNA序列 187题:
所有 DNA 由一系列缩写为 A,C,G 和 T 的核苷酸组成,例如:“ACGAATTCCG”。在研究 DNA 时,识别 DNA 中的重复序列有时会对研究非常有帮助。
编写一个函数来查找 DNA 分子中所有出现超多一次的10个字母长的序列(子串)。
示例:
输入: s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
输出: ["AAAAACCCCC", "CCCCCAAAAA"]
分析:
这题需要遍历所有长度为10的子串是无法避免的(一共有n-9个长度为10的子串)。在遍历的同时要判断重复出现要用到哈希表;但是是要找出重复出现的子串,这时就还要用另一个哈希表(由于最后的结果中肯定不能有重复,所以还是选用哈希表)存放重复出现的子串,而第一个哈希表只起到判断重复的作用。
这题还有一种位运算的解法可以节省空间(哈希表中不存String存Integer)
代码:
public List<String> findRepeatedDnaSequences(String s) {
Set seen = new HashSet(), repeated = new HashSet();
for (int i = 0; i + 9 < s.length(); i++) {
String ten = s.substring(i, i + 10);
if (!seen.add(ten))
repeated.add(ten); //遇到重复子串添加到结果,repeated是哈希表是为了防止结果重复
}
return new ArrayList(repeated); //用hashset初始化arraylist
}
同构字符串 205题:
给定两个字符串 s 和 t,判断它们是否是同构的。
如果 s 中的字符可以被替换得到 t ,那么这两个字符串是同构的。
所有出现的字符都必须用另一个字符替换,同时保留字符的顺序。两个字符不能映射到同一个字符上,但字符可以映射自己本身。
示例:
输入: s = "egg", t = "add"
输出: true
输入: s = "foo", t = "bar"
输出: false
输入: s = "paper", t = "title"
输出: true
分析:
这道题可以用建两个Hashmap来做,一个s的,一个t的;key存字符,value存下标;每次put时,比较各自旧的value值(即之前的下标)是否相等,不等直接返回false,遍历一遍返回true。
注意到其实这题中的字符实际上是有限个(ASCII字符一共256个),而且字符的值可以用作索引,所以可以用数组(也是常用方法);建一个512长度的数组(前256个位置用于s字符串,后256个位置用于t字符串),数组中存相应字符上一次出现的下标+1。
代码:
public boolean isIsomorphic(String s1, String s2) {
Map<Character, Integer> m1 = new HashMap<>();
Map<Character, Integer> m2 = new HashMap<>();
for(Integer i = 0; i < s1.length(); i++) {//注意这里只能用Integer
if(m1.put(s1.charAt(i), i) != m2.put(s2.charAt(i), i)) {
//这里put函数返回值:与 key 关联的旧value;如果 key 没有任何映射关系,则返回 null。
return false;
}
}
return true;
}
/*对于只能用Integer i=0,不能写成int i=0;属于java中Integer包装类中的一个知识,
由于Integer i 是一个对象,用!=比较时,比较的是不是同一个引用,不是比较的i的值等不等,int i每次自动生成对应的包装类时都新生成了不同的对象(即便i的值相等)。
那为什么有时却是可以的?因为当int i 的值为-128到127时,不会生成新的不同的对象,而是使用池中对应的对象,这时候int的值相等时,包装后的Integer都是同一个对象,所以就能用!=判断不等。
*/
数组的解法:
public class Solution {
public boolean isIsomorphic(String s1, String s2) {
int[] m = new int[512];
for (int i = 0; i < s1.length(); i++) {
if (m[s1.charAt(i)] != m[s2.charAt(i)+256]) return false;
m[s1.charAt(i)] = m[s2.charAt(i)+256] = i+1;
}
return true;
}
}
/* m[s1.charAt(i)] = m[s2.charAt(i)+256] = i+1;
这一步为什么是i+1?因为数组中默认都是0,标记下标如果从0开始,不区分默认和后置的标记下标会出错;
例如:“aa”和“ab”
*/
单词模式 290题:
给定一种 pattern(模式) 和一个字符串 str ,判断 str 是否遵循相同的模式。
这里的遵循指完全匹配,例如, pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应模式。
示例:
输入: pattern = "abba", str = "dog cat cat dog"
输出: true
输入:pattern = "abba", str = "dog cat cat fish"
输出: false
分析:
这题跟同构字符串那题实际是一样的,不过parrern和str要进行匹配的类型不同了,一个是字符,一个是子字符串,所以不能用数组的方法了,用哈希表的方法做。
代码:
public boolean wordPattern(String pattern, String str) {
String[] words = str.split(" "); //将str以空格分割开存入string数组
if (words.length != pattern.length()) //长度不等直接退出
return false;
Map index = new HashMap();
//哈希表中存两种键值对 (Charact,Integer)和(String,Integer)之间互不影响
for (Integer i=0; i<words.length; ++i)
if (index.put(pattern.charAt(i), i) != index.put(words[i], i))
//put函数返回值为以前与key关联的value,映射以前包含一个该键的映射关系,则用指定值替换旧值
return false;
return true;
}
/*
遍历 在这里i被设置为Integer而不是int是因为如果设为int则要自动装箱,
而同一int值自动装箱后的生成的Integer在用==比较时不一定相等。
(只有在-128到127才等 The JVM is caching Integer values. == only works for numbers between -128 and 127)
*/
猜数字游戏 299题:
你正在和你的朋友玩 猜数字(Bulls and Cows)游戏:你写下一个数字让你的朋友猜。每次他猜测后,你给他一个提示,告诉他有多少位数字和确切位置都猜对了(称为“Bulls”, 公牛),有多少位数字猜对了但是位置不对(称为“Cows”, 奶牛)。你的朋友将会根据提示继续猜,直到猜出秘密数字。
请写出一个根据秘密数字和朋友的猜测数返回提示的函数,用 A 表示公牛,用 B 表示奶牛。
请注意秘密数字和朋友的猜测数都可能含有重复数字
示例:
输入: secret = "1807", guess = "7810"
输出: "1A3B"
解释: 1 公牛和 3 奶牛。公牛是 8,奶牛是 0, 1 和 7。
分析:
这里Bulls的统计比较容易,一次遍历比较就行;对于cows,除了Bulls外,只要secret中有的数字guess中也有,那么对应的这个数字的cows就是这个数字公共出现的个数,例如,除去Bulls不看,secret中有2个‘1’,guess中有1个‘1’,那么‘1’这个字符的cows就是1,再继续看其他数字把cows加起来。
这里需要统计每次数字出现的个数,要定义一些计数器,不妨建两个长度为10的数组来计数。
代码:
public String getHint(String secret, String guess) {
int temp = 0;
int bulls = 0;
int[] nums1 = new int[10]; //存secret中的除了能对应上的其他数字的个数 如nums[0]为secret中除了对应上的
//其余0的个数
int[] nums2 = new int[10]; //同上 存guess中的
for(int i = 0; i < secret.length(); i++){
char s = secret.charAt(i);
char g = guess.charAt(i);
if(s == g){
bulls++; //对应相等 bulls直接就加
}
else{
nums1[s - '0']++; //否则俩个数组相应位置上+1
nums2[g - '0']++;
}
}
int cows = 0;
for(int i = 0; i < 10; i++){
cows += Math.min(nums1[i], nums2[i]); //遍历一遍俩数组 cows每次加上两数组中相应数字公共出现的次数
}
String res = bulls + "A" + cows + "B";
return res;
}
数字中的问题
分数到小数 166题:
给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以字符串形式返回小数。
如果小数部分为循环小数,则将循环的部分括在括号内。
示例:
输入: numerator = 1, denominator = 2
输出: "0.5"
输入: numerator = 2, denominator = 1
输出: "2"
输入: numerator = 2, denominator = 3
输出: "0.(6)"
分析:
示例中的三种就是要考虑的所有情况。即能够整除,只有整数位,循环小数。这三种中只有整数位最好处理,有循环最最复杂;如何判断循环?有循环就意味着重复,所以,哈希表。
注意这里可能会有溢出的问题,所以将int转化为long
代码:
public String fractionToDecimal(int numerator, int denominator) {
if (numerator==0) return "0";
StringBuilder res=new StringBuilder();
res.append((numerator>0)^(denominator>0)?"-":"");
long num=Math.abs((long) numerator); //转成long防止溢出
long den=Math.abs((long)denominator);
res.append(num/den);
num=num%den;
if (num==0){
return res.toString(); //能整除没小数部分就返回就行
}
res.append("."); //否则有小数部分 先加个小数点
Map<Long,Integer> map=new HashMap<>(); //建哈希表存余数是关键
map.put(num,res.length()); //key是余数 value存的是下标,以便循环时插入()
while (num!=0){
//判断余数是否为0 为零说明就除净了,在while中num也不总是存余数,也做被除数用,
//但一定是判断余数是否为零,while中的语句结构顺序很重要
num*=10; //类似列竖式做除法 余数乘10再除以除数
res.append(num/den);
num%=den;
if (map.containsKey(num)){
int index=map.get(num);
res.insert(index,"(");
res.append(")");
break;
}else {
map.put(num,res.length());
}
}
return res.toString();
}
快乐数 202题(easy):
编写一个算法来判断一个数是不是“快乐数”。
一个“快乐数”定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果可以变为 1,那么这个数就是快乐数。
示例:
输入: 19
输出: true
解释:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
分析:
这题和分数到小数有点类似,都是用哈希表判断重复数字进而判断循环。可以写一个数字求和的辅助函数,方法就是% /这种。
代码:
public boolean isHappy(int n) {
Set<Integer> set=new HashSet<>();
int a;
while (set.add(n)){
a=qiuhe(n);
if (a==1){
return true;
}
else n=a;
}
return false;
}
public int qiuhe(int m){
int x,b=0;
while (m>0){
x=m%10;
b=b+x*x;
m=m/10;
}return b;
}
计数质数 204(easy):
统计所有小于非负整数 n 的质数的数量。
示例:
输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
分析:
这题有一个经典算法,叫 埃拉托色尼筛选法(Sieve of Eratosthenes算法)
步骤如下:
(1)先把1删除(1既不是质数也不是合数)
(2)读取队列中当前最小的数2,然后把2的倍数删去
(3)读取队列中当前最小的数3,然后把3的倍数删去
(4)读取队列中当前最小的数5,然后把5的倍数删去
.......
(n)读取队列中当前最小的状态为true的数n,然后把n的倍数删去
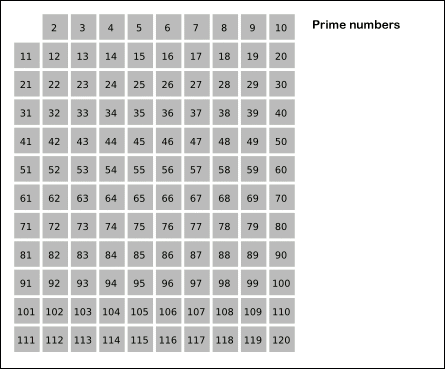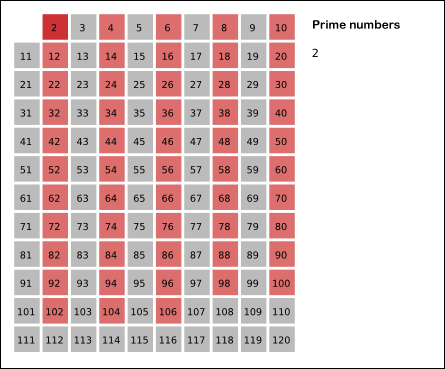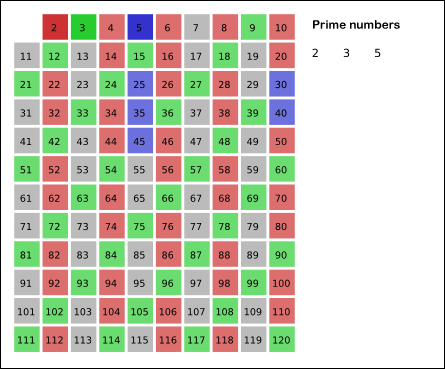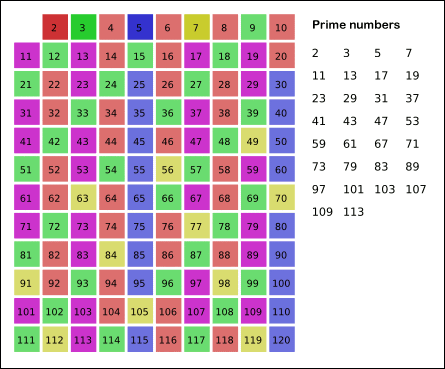
这题呢,能用哈希表做,思路是将所有数存哈希表中,再把非质数remove掉,但会超时。
实际只需要建一个n长的boolean数组就行了。不知道这题为什么有哈希表的标签....
代码:
public int countPrimes(int n) {
boolean[] notPrime = new boolean[n];
int count = 0;
for (int i = 2; i < n; i++) {
if (notPrime[i] == false) {
count++;
for (int j = 2; i*j < n; j++) {
notPrime[i*j] = true;
}
}
}
return count;
}
遗留问题:
18.四数之和 (双指针)
94.二叉树中序遍历 (树)
136.只出现一次的数字(位运算)
274.H指数(sort 计数排序)