计数排序

思路：

我们先假设待排序序列各元素均在区间[0, k]上。
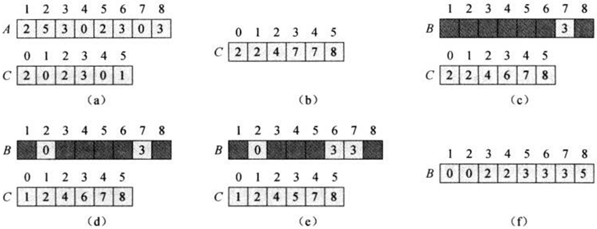
思想是：在待排序序列中，如果我们能统计出有多少元素小于或等于某一个元素，我们也就知道了该元素的正确位置。例如，对于待排序序列{2,5,3,0,2,3,0,3}，我们统计出有8个元素小于等于5（包括5自己），那么5这个元素就应该被排序到第8位。

伪代码：

其中数组A[1_{n]是待排序数组；数组B[1}n]用来存放已排好序的元素。C[0~k]用来存放上面所说的统计数（具体的说C[i]就表示在数组A中，小于或等于i的元素的总个数）。

图解：

java代码：

public static int[] countingSort(int[] array, int max) {
	int[] result = new int[array.length];
	int[] temp = new int[max + 1];
	// 以下循环操作完成后，temp的第i个位置保存着array中，值为i的元素的总个数
	for (int i : array) {
		temp[i]++;
	}
	// 以下循环操作完成后，temp的第i个位置保存着array中，值小于或等于i的元素的总个数
	for (int i = 1; i < temp.length; i++) {
		temp[i] += temp[i - 1];
	}
	for (int i = array.length - 1; i > -1; i--) {
		result[temp[array[i]] - 1] = array[i];
		temp[array[i]]--;
	}
	return result;
}

复杂度：θ(k+n)

在伪代码中，第2~3行时间代价θ(k)；第4~5行时间为θ(n)；第7~8行时间为θ(k)，第10~12行时间为θ(n)。因此，总的运行时间是θ(k+n)。当k= O(n)时，运行时间为θ(n)。
可以看出，计数排序的下界优于我们上面论证的比较排序算法的下界时间Ω(nlgn)。这是因为计数排序并不是比较排序算法。事实上，在代码中从未出现比较某两个元素大小的代码。相反，计数排序是使用输入元素的实际值来确定其在数组中的位置。此时，比较排序算法的模型对计数排序不再适用。