J.Easy Integration
公式题,沃利斯积分:(int_{0}^{1}{(x-x^2)^n}dx=frac{(n!)^2}{(2n+1)!})
一直按照分部积分公式:(int{u(x)v'(x)dx}=u(x)v(x)-int{u'(x)v(x)dx})
推导:
(int_{0}^{1}{(x-x^2)^n}dx)
(=frac{1}{n+1}int_{0}^{1}{[x^{n+1}]' (1-x)^n dx})
(=frac{1}{n+1}(x^{n+1}(1-x)^n|_0^1-int_{0}^{1}{x^{n+1}[(1-x)^n]'}dx))
(=frac{n}{n+1}int_{0}^{1}{x^{n+1}(1-x)^{n-1}}dx)
以此类推,可得:
(frac{n*(n-1)*...*1*int_{0}^{1}{x^{2n}}}{(n+1)*(n+2)*...*(2n)})
(=frac{n!}{(n+1)*...*(2n+1)})
(=frac{(n!)^2}{(2n+1)!})
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int N=1e6+6;
const int maxn=2e6+1;
ll f[N<<1],inv[N<<1];
ll power(ll a,ll b)
{
ll res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
void init()
{
f[0]=1;//阶乘
for(int i=1;i<=maxn;i++)
f[i]=f[i-1]*i%mod;
for(int i=0;i<=maxn;i++)//1!~(2n+1)!逆元
inv[i]=power(f[i],mod-2);
}
int main()
{
init();
int n;
while(scanf("%d",&n)!=EOF)
{
ll ans=f[n]*f[n]%mod*inv[2*n+1]%mod;
printf("%lld
",ans);
}
return 0;
}
I.1 or 2
解1:
拆点,求最大匹配。
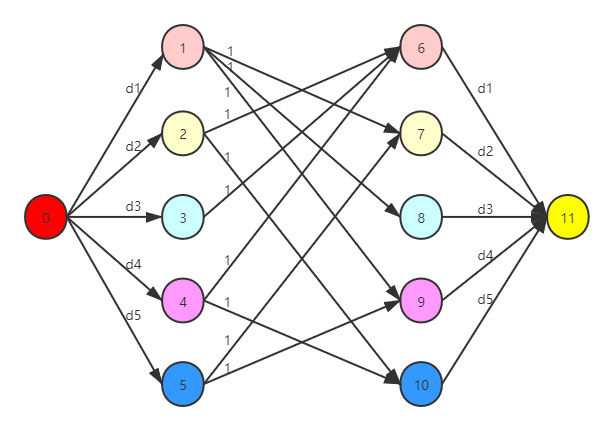
但这样写,应该有问题的。不能保证上次从点 (u) 取了和 (v) 之间的边,下次从 (v) 就会取和 (u) 之间的边。
比如下面的图就就有问题
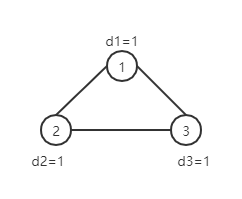
应该输出 (No),但输出了 (Yes)。
代码1:
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=110;
const int inf=0x3f3f3f3f;
struct node
{
int to,val,rev;//边的终点,边的容量,方向边的索引
};
vector<node>pic[N<<1];
queue<int>que;
int layer[N<<1],iter[N<<1];//iter[]数组用于当前弧优化
int vn,s,t;
bool bfs()
{
for(int i=0;i<=vn;i++)
layer[i]=-1;
while(!que.empty())
que.pop();
layer[s]=0;
que.push(s);
while(!que.empty())
{
int a=que.front();
que.pop();
for(int i=0;i<pic[a].size();i++)
{
node b=pic[a][i];
if(layer[b.to]<0&&b.val>0)//layer[]相对于标记
{
layer[b.to]=layer[a]+1;
que.push(b.to);
if(b.to==t)//不用把所有的点都分层,只要分到汇点就行
return true;
}
}
}
return false;
}
int dfs(int a,int c)//
{
if(a==t)
return c;
for(int &i=iter[a];i<pic[a].size();i++)//当前弧优化,已经用过非边不再遍历,引用
{
node &e=pic[a][i];//引用,后面可以直接修改数据
if(e.val>0&&layer[e.to]>layer[a])//只走后面的层次的点
{
int d=dfs(e.to,min(c,e.val));//每次找到一条增广路后,一直回溯到起点,并在此过程中确定路上的最小流量
if(d>0)
{
e.val-=d;
pic[e.to][e.rev].val+=d;//改变时要对原来的信息修改
return d;//返回该条增广路的最大流
}
}
}
return 0;//
}
int dinic()
{
int max_flow=0;
while(bfs())
{
int f=0;
memset(iter,0,sizeof(iter));
while((f=dfs(s,inf))>0)
max_flow+=f;
}
return max_flow;
//printf("%d
",max_flow);
}
void add(int u,int v,int w)
{
pic[u].pb({v,w,pic[v].size()});
pic[v].pb({u,0,pic[u].size()-1});
}
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)!=EOF)
{
int d=0,tol=0;
vn=2*n+1;
s=0,t=vn;
for(int i=0;i<=vn;i++)
pic[i].clear();
for(int i=1;i<=n;i++)
{
scanf("%d",&d);
tol+=d;
add(0,i,d);
add(i+n,vn,d);
}
int u,v;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add(u,v+n,1);
add(v,u+n,1);
}
int ans=dinic();//cout<<"ans="<<ans<<endl;cout<<"tol="<<tol<<endl;
if(ans==tol) printf("Yes
");
else printf("No
");
}
return 0;
}
代码2:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
typedef pair<int,int>pii;
const int N=55;
int d[N],a[N];
vector<pii>pic[N];
bool vis[N<<1];
int n,m;
bool cmp(int x,int y)
{
return pic[x].size()<pic[y].size();
}
bool dfs(int k)
{
if(k>n) return 1;
if(d[a[k]]==0) return dfs(k+1);//该电的度已满足,找下一个点
for(int i=0;i<pic[a[k]].size();i++)
{
int u=pic[a[k]][i].first;
int e=pic[a[k]][i].second;
if(vis[e]||d[u]==0) continue;//边走过或者该点的度已经满足
d[a[k]]--,d[u]--,vis[e]=1;
bool f=dfs(k);
if(f) return 1;
vis[e]=0,d[a[k]]++,d[u]++;
}
return 0;
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)
{
memset(vis,false,sizeof(vis));
for(int i=1;i<=n;i++)
{
scanf("%d",&d[i]);
a[i]=i;
pic[i].clear();
}
int u,v;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
pic[u].pb(make_pair(v,i));
pic[v].pb(make_pair(u,i));
}
sort(a+1,a+1+n,cmp);//把点按度排序
if(dfs(1)) printf("Yes
");
else printf("No
");
}
return 0;
}