2018ACM-ICPC焦作站E题Resistors in Parallel

Resistors in Parallel

题目：

       ACM-ICPC Jiaozuo Onsite 2018

    

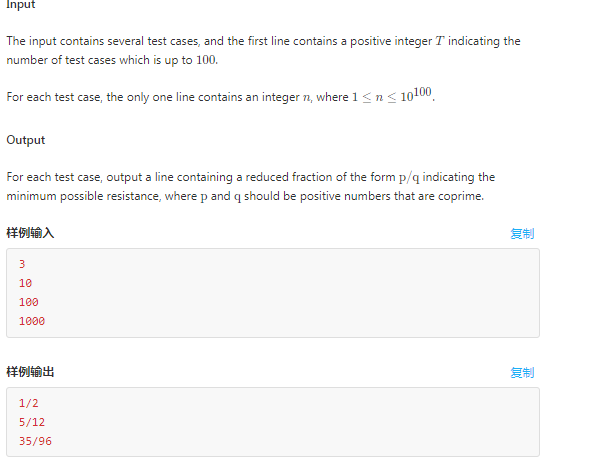
题解：因为题目数据范围很大，所以猜测应该是一个区间一个固定的最小值。问题转换成了如何求某个最小值影响的区间。坤神一眼看出，应该通过素数求，因为一个数的因子有很多，但是所有的因子都可以通过该数的素因子推出来。比如6的因子有1 2 3 6，素因子有2 3，所以1=2^0*3^0,2=2^1*3^0,3=2^0*3^1,6=2^1*3^1。又因为并联电阻并联越多阻值越小，所以在某些数有相同的素因子的情况下，这些素因子组成的因子越多越好，但是题目说能被d*d （d>=2）整除的因子的电阻为无穷大，并联相当于没有，所以对总电阻的贡献值为0，可以不考虑。所以以30为例，30的素因子有2 3 5，所以我们只需要计算x=1+2+3+5+2*3+2*5+3*5+2*3*5,(计算这个也是找规律，2 3 5中有 1个1 1个2 1+1*2个3 1+2+（1+2）*3个5……每个存在的素因子的个数为前面所有素数的总和（orz贤哥tql）)即可，然后只以2 3 5为素因子的区间最小值就是30/gcd(30,x) / (x/(gcd(30,x))).最后对于每次输入的N,以素数从小到大累乘的方式找到n以内数最大组成的素因子。例如n=100 2*3*5<=100,2*3*5*7>100,所以100就在只以2 3 5为素因子的区间里。

因为这个题的数据范围很大，所以用Java写。

import java.util.*;
import java.math.*;
public class Main{
    static Scanner cin = new Scanner(System.in);
    static BigInteger [] dp = new BigInteger[1100];
    static boolean [] prime = new boolean[11000];
    static int[] nums = new int [11000];
    static int cnt = 0;
    public static void init() {
        prime[1] = true;
        for(int i = 1 ;i<=1000;i++) {
            prime[i]=true;
        }
        for(int i = 2; i <= 1000; i++) {
            if(prime[i]) {
                nums[++cnt] = i;
                for(int j = i+i; j <= 1000; j +=i) {
                    prime[j] = false;
                }
            }
        } 
    }
    public static void main(String[] args) {
        init();
        int casen = cin.nextInt();
        while(casen-->0) {
            BigInteger n = cin.nextBigInteger();
            int k;
            dp[0] = BigInteger.ONE;
            BigInteger yinzi = BigInteger.ONE;  
            for(k = 1; (yinzi.multiply(BigInteger.valueOf(nums[k])).compareTo(n)<=0);k++) {
                yinzi = yinzi.multiply(BigInteger.valueOf(nums[k]));
            } 
            k--;
            BigInteger sum = BigInteger.ONE;
            for(int i = 1;i <= k; i++) {
                dp[i]=dp[i-1].add(dp[i-1].multiply(BigInteger.valueOf(nums[i])));
            }
            BigInteger gcd = yinzi.gcd(dp[k]);
            System.out.println(yinzi.divide(gcd)+"/"+dp[k].divide(gcd));
        }
    }

}