二叉树

前言: 这篇博客较详细介绍了二叉树，写得没什么难度，主要是为了我自己总结。二叉树是我大二上数据结构学的，当时刚转专业到计科，对指针啥的很懵逼。so, 学得很拼但效果相当一般。之后会写一些关于二叉树的算法，敬请关注......

一、基本概念

1. 二叉树的结点包含一个数据元素及指向其左右子树的两个分支，分别称为左分支和右分支。
2. 结点的孩子个数称为结点的度(degree)。
3. 度为0的结点称为叶子结点(leaf)。
4. 结点的层次(level): 根为第1层，根的孩子为第2层，如此计算，直到叶子结点为至。
5. 二叉树中结点的最大层次称为二叉树的深度/高度(depth/height)。

下图: 8为根结点；1、5、7、9为叶子结点；二叉树的深度为4.

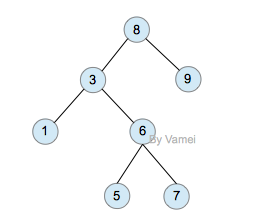
二叉树是由n（n≥0）个结点组成的有限集合、每个结点最多有两个子树。它或者是空集，或者是由一个根和称为左、右子树的两个不相交的二叉树组成。

特点：

（1）二叉树可以为空树；即使只有一个子树，也必须区分左、右子树；

（2）二叉树的每个结点的度不能大于2，只能取0、1、2三者之一；

（3）二叉树中所有结点的形态有5种：空结点、无左右子树的结点、只有左子树的结点、只有右子树的结点和具有左右子树的结点。

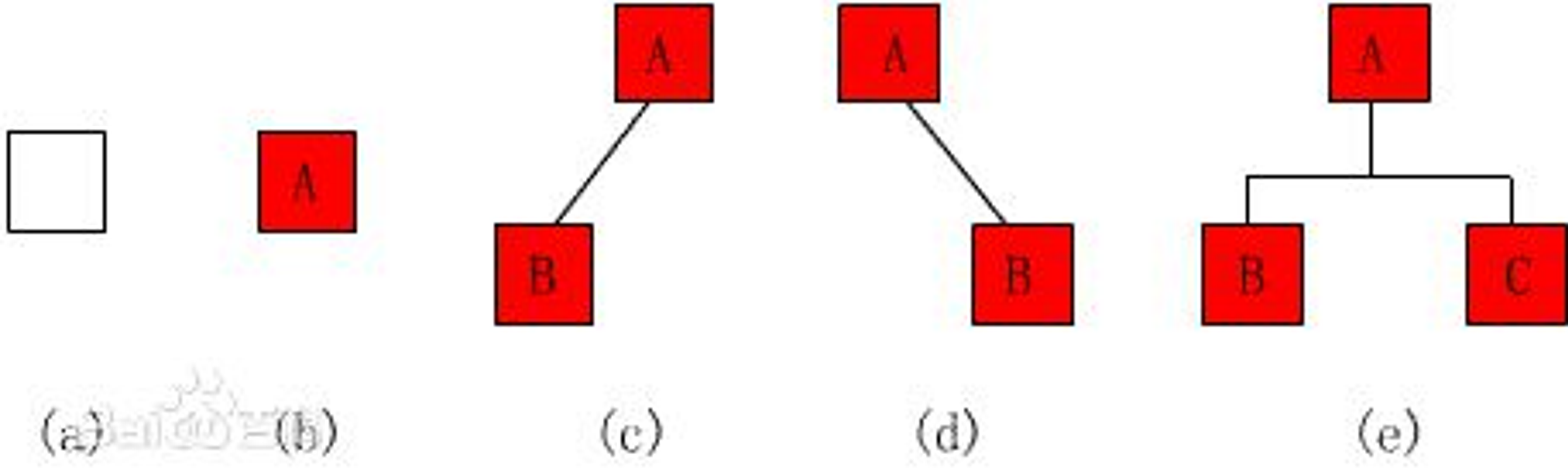
二、性质

二叉树中有5点性质非常重要，也是必须要记住的。

1. 二叉树中，第i层的节点最多有2^(i-1)个。
2. 深度为k的二叉树最多有2^k-1个节点。
3. 二叉树中，叶子节点树为N₁个，度为2的节点有N₂个，那么N₁=N₂+1。
4. 具有N个结点的二叉树深度为（Log₂ N）+1层。
5. N个结点的完全二叉树如何用顺序存储，对于其中的一个结点i，存在以下关系，
   • 2*i是结点i的父结点。
   • i/2是结点i的左孩子。
   • (i/2)+1是结点i的右孩子。

三、二叉树的类型

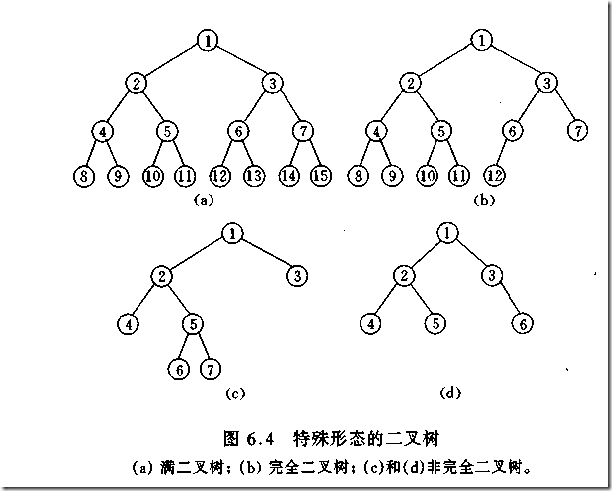
(1)完全二叉树(complete binary tree)－－若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树(full binary tree)－－除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)二叉查找树(binary search tree)－－每个节点都不比它左子树的任意元素小，而且不比它的右子树的任意元素大。

(如果我们假设树中没有重复的元素，那么上述要求可以写成：每个节点比它左子树的任意节点大，而且比它右子树的任意节点小)

(4)平衡二叉树(balanced binary sort tree)——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树binary sort tree(二叉查找树)，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

下图为二叉查找树:

满二叉树与完全二叉树:

如何判断平衡二叉树:

首先你得懂二叉树结点的平衡因子: 该结点的左子树高度减去它的右子树高度，则平衡二叉树上所有结点的平衡因子只可能为-1、0、1

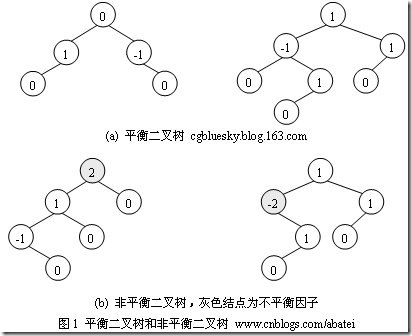
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0  右子树的高度为2，相差超过1

四、 二叉树的存储结构

存储二叉树时，除了存储它的每个结点数据外，结点之间的逻辑关系(父子关系)也要得到体现。下面介绍 “顺序存储” 和 “链式存储”。

图参考自: http://blog.csdn.net/zeroyl/article/details/11580447

顺序存储

二叉树的顺序存储，就是用一组连续的存储单元存放二叉树中的结点。因此，必须把二叉树的所有结点安排成为一个恰当的序列，结点在这个序列中的位置能反映出结点之间的逻辑关系。

依据二叉树的性质，完全二叉树和满二叉树采用顺序存储比较合适，树中结点的序号可以唯一地反映出结点之间的逻辑关系，这样既能够最大可能地节省存储空间，又可以利用数组元素的下标值确定结点在二叉树中的位置，以及结点之间的关系。

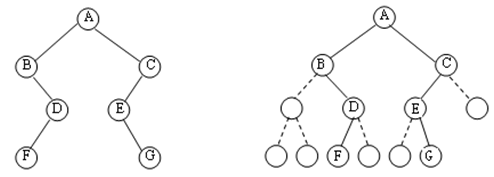
现在给下图右边数组，你能画出左边的树结构??反之你能画出数组内容??

 　　　(a)一棵完全二叉树                  　　　　　(b)顺序存储结构(0号单元不用)

很简单啊! 比如我拿右边的下标为2的数据B，它父亲的下标为int(i/2)=1, 即:A。它的左孩子为2*2=4, 即D; 右孩子为2*2+1=5, 即E. 其它同理。你懂得。

　　(a) 一棵二叉树                          　　　(b) 改造后的完全二叉树

显然，这种存储对于需增加许多空结点才能将一棵二叉树改造成为一棵完全二叉树的存储时，会造成空间的大量浪费，不宜用顺序存储结构。

 

链式存储

一个结点存放着一个“左指针”和一个“右指针”，这就是二叉链表。

每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。其结点结构为：

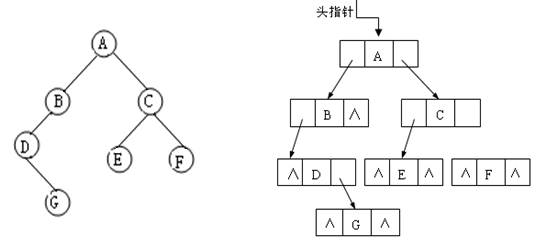
　　　　(a) 一棵二叉树                       　　 (b) 二叉链表存储结构

为了方便访问某结点的双亲，还可以给链表结点增加一个双亲字段parent,用来指向其双亲结点。

这种存储结构既便于查找孩子结点，又便于查找双亲结点；但是，相对于二叉链表存储结构而言，它增加了空间开销。利用这样的结点结构表示的二叉树的链式存储结构被称为三叉链表。

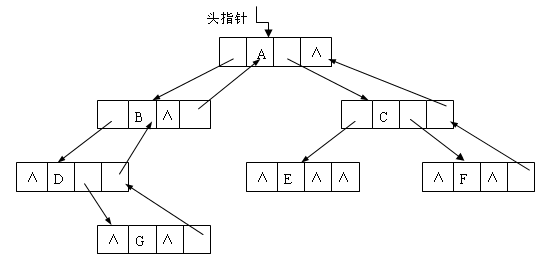
　　　　　　　　　　　　　二叉树的三叉链表表示示意图