汉诺塔问题（Hanoi Tower）递归算法解析（Python实现）

汉诺塔问题

1.问题来源：汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三根金刚石柱子，在一根柱子上从上往下从小到大顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一回只能移动一个圆盘，只能移动在最顶端的圆盘。

2.问题分析：

汉诺塔问题的以下几个限制条件：

1.在小圆盘上不能放大圆盘。

2.在三根柱子之间一回只能移动一个圆盘。

3.只能移动在最顶端的圆盘。

 

案例 1 - 假设只有一个盘子的时候, 盘子数量 N=1

 

只有一个步骤   将第1个盘子从A移动到C, 为了对比方便我这样来描述这个步骤：

 

步骤  盘子编号 从柱子移动   移动到柱子

 

1       1                A               C

 

案例 2 - 如果有两个盘子, 盘子数量 N = 2

 

步骤  盘子编号 从柱子移动   移动到柱子

 

1              1                A               B

 

2              2                A               C

 

3              1                B               C

 

案例 3  - 如果有三个盘子, 盘子数量 N = 3

 

步骤      盘子编号     从柱子移动     移动到柱子

 

1                1　　　    A                     C

 

2                2　　　    A　　　　       B

 

3                1              C                     B

 

4                3              A                    C

 

5                1              B                    A

 

6                2              B                    C

 

7                1              A                    C   

 

观察第3个案例中的第 1-3 步 和 第 5-7步

 

第 1-3 步 目的是从 A 移动到 B   如果我们把 B 当作终点, 那么这里的第 1-3 步理解起来和 第2个案例的三个步骤完全相同

 

1       1　　　  A           C     ( A -> B)

 

2       2　　　  A　       B     ( A -> C)

 

3       1              C           B      ( B -> C)

 

总结：将盘子B变成C即可.

第 5-7 步 目的是从 B 移动到 C   如果我们把 C 当作终点, 那么这里的 5-7 步理解起来和上面也是一样的, 和第2个案例的三个步骤也完全相同.和第2个案例比起来就是:

 

5       1       B           A    ( A -> B)

 

6       2       B           C    ( A- > C)

 

7       1       A           C    ( B -> C)

 

 

 

总结: 将盘子B变成A即可

 

根据这个演示可以明确几点规律：

 

1. 当盘子只有一个的时候,只有一个动作 从 A 移动到 C 即结束.

 

2. 当有N个盘子的时候, 中间的动作都是从 A 移动到 C, 那么表示最下面的第N个盘子移动完毕

 

3. 中间动作之上都可以认为是: 从 A 移动到 B

 

4. 中间动作之下都可以认为是: 从 B 移动到 C

 

 

 

3.代码实现

 

 

# -*- coding: utf-8 -*-
# Hanoi_Tower.py
# @author  0yst3r
# @description
# @created Tue Apr 16 2019 11:25:35 GMT+0800 (中国标准时间)
# @last-modified Tue Apr 16 2019 14:29:13 GMT+0800 (中国标准时间)
#

i = 0


def Num():
    global i
    i = i + 1
    return i


def move(n, a, b, c):
    if n == 1:
        print(a, '->', c)
        Num()

    else:
        move(n - 1, a, c, b)
        print(a, '->', c)  # move(1, a, b, c)
        move(n - 1, b, a, c)
        Num()


n = eval(input("请输入盘子的个数:"))
print('移动步骤如下：')
print(move(n, 'A', 'B', 'C'))
print('移动总次数为：', i)

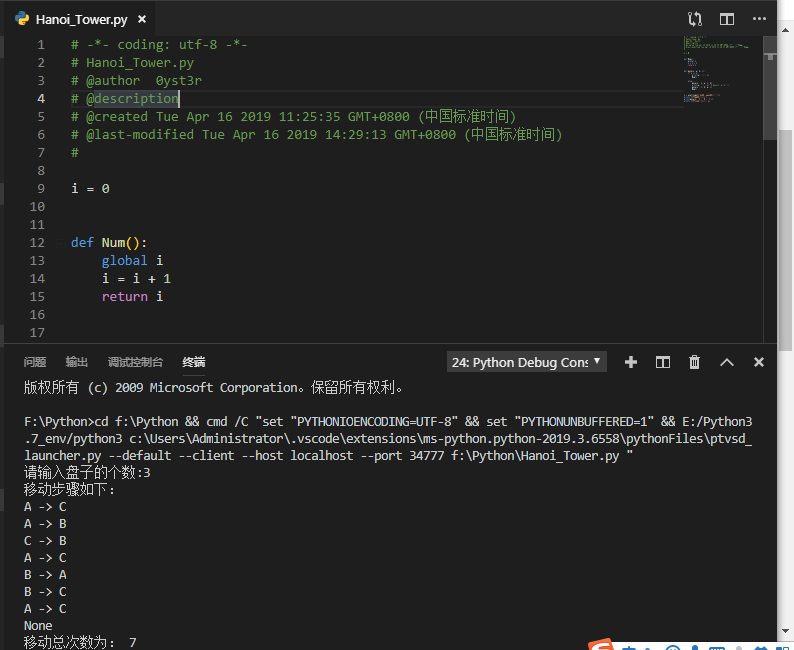
运行结果：

输入 n=3

 

 4.参考资料

https://www.cnblogs.com/antineutrino/p/3334540.html

https://blog.csdn.net/liujian20150808/article/details/50793101