2019春第十一周作业
2019春第十一周作业:
| 作业所属科目 | C语言程序设计 | ||
| 作业所需要求 | 第十一周作业 | ||
| 我在这个课程的目标是 | 学会结构 宏的定义 递归算法 | ||
|
这个作业在哪个具体方面帮助我实现目标 参考文献 |
|
7-1 汉诺塔问题* (10 分)
汉诺塔是一个源于印度古老传说的益智玩具。据说大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘,大梵天命令僧侣把圆盘移到另一根柱子上,并且规定:在小圆盘上不能放大圆盘,每次只能移动一个圆盘。当所有圆盘都移到另一根柱子上时,世界就会毁灭。

请编写程序,输入汉诺塔圆片的数量,输出移动汉诺塔的步骤。
输入格式:
圆盘数 起始柱 目的柱 过度柱输出格式:
移动汉诺塔的步骤
每行显示一步操作,具体格式为:
盘片号: 起始柱 -> 目的柱
其中盘片号从 1 开始由小到大顺序编号。输入样例
3
a c b输出样例
1: a -> c
2: a -> b
1: c -> b
3: a -> c
1: b -> a
2: b -> c
1: a -> c1)实验代码:
nt main (void) { int n; char a,b,c; scanf("%d ",&n); scanf("%c %c %c",&a, &b, &c); hanio (n,a,b,c); return 0; } void hanio (int n,char a,char b,char c) { if(n==1) printf("%d: %c -> %c ",n,a,b); else { hanio(n-1,a,c,b); printf("%d: %c -> %c ",n,a,b); hanio(n-1,c,b,a); } }
2)流程图
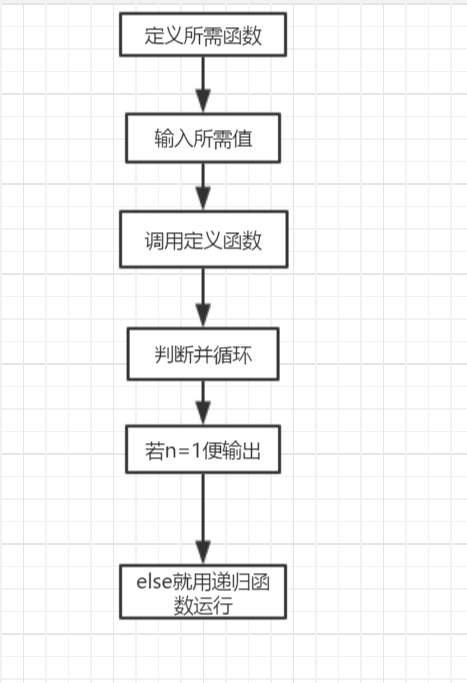
3)遇到的问题和错误的截图以及解决方法
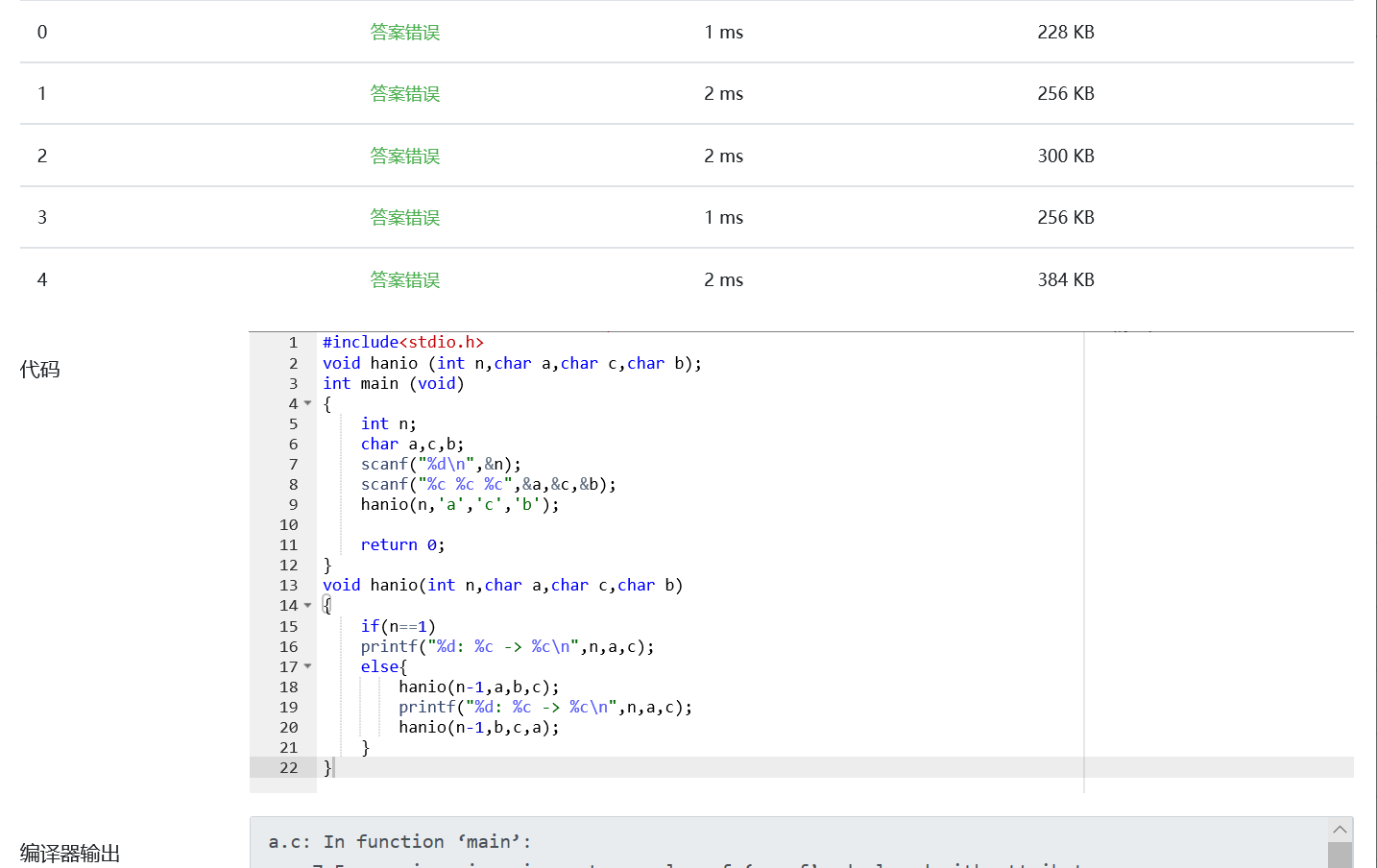
由于忘记成功截图了,到了时间了不能显示出正确截图,就把代码截图了:

7-2 估值一亿的AI核心代码 (20 分)
本题要求你实现一个稍微更值钱一点的 AI 英文问答程序,规则是:
- 1:无论用户说什么,首先把对方说的话在一行中原样打印出来;
- 2:消除原文中多余空格:把相邻单词间的多个空格换成 1 个空格,把行首尾的空格全部删掉,把标点符号前面的空格删掉;
- 3:把原文中所有大写英文字母变成小写,除了 I;
- 4:把原文中所有独立的 can you、could you 对应地换成 I can、I could—— 这里“独立”是指被空格或标点符号分隔开的单词;
- 5:把原文中所有独立的 I 和 me 换成 you;
- 6:把原文中所有的问号 ? 换成惊叹号 !;
-
7:在一行中输出替换后的句子作为 AI 的回答。
输入格式:
输入首先在第一行给出不超过 10 的正整数 N,随后 N 行,每行给出一句不超过 1000 个字符的、以回车结尾的用户的对话,对话为非空字符串,仅包括字母、数字、空格、可见的半角标点符号。输出格式:
按题面要求输出,每个 AI 的回答前要加上 AI: 和一个空格。
输入样例:
6
Hello ?
Good to chat with you
can you speak Chinese?
Really?
Could you show me 5
What Is this prime? I,don 't know输出样例:
Hello ?
AI: hello!
Good to chat with you
AI: good to chat with you
can you speak Chinese?
AI: I can speak chinese!
Really?
AI: really!
Could you show me 5
AI: I could show you 5
What Is this prime? I,don 't know
AI: what Is this prime! you,don't know1)实验代码:
这个题目不会做,只会做第一个
挑战题
7-3 ***八皇后问题 (20 分)
在国际象棋中,皇后是最厉害的棋子,可以横走、直走,还可以斜走。棋手马克斯·贝瑟尔 1848 年提出著名的八皇后问题:即在 8 × 8 的棋盘上摆放八个皇后,使其不能互相攻击 —— 即任意两个皇后都不能处于同一行、同一列或同一条斜线上。
现在我们把棋盘扩展到 n × n 的棋盘上摆放 n 个皇后,请问该怎么摆?请编写程序,输入正整数 n,输出全部摆法(棋盘格子空白处显示句点“.”,皇后处显示字母“Q”,每两格之间空一格)。
输入格式
正整数 n (0 < n ≤ 12)
输出格式
若问题有解,则输出全部摆法(两种摆法之间空一行),否则输出 None。
要求:试探的顺序逐行从左往右的顺序进行,请参看输出样例2。
输入样例1
3输出样例1
None输入样例2
6输出样例2
. Q . . . .
. . . Q . .
. . . . . Q
Q . . . . .
. . Q . . .
. . . . Q .
. . Q . . .
. . . . . Q
. Q . . . .
. . . . Q .
Q . . . . .
. . . Q . .
. . . Q . .
Q . . . . .
. . . . Q .
. Q . . . .
. . . . . Q
. . Q . . .
. . . . Q .
. . Q . . .
Q . . . . .
. . . . . Q
. . . Q . .
. Q . . . .
7-1 求迷宫最短通道 (20 分)
递归求解迷宫最短通道的总步长。输入一个迷宫,求从入口通向出口的可行路径中最短的路径长度。为简化问题,迷宫用二维数组 int maze[10][10]来存储障碍物的分布,假设迷宫的横向和纵向尺寸的大小是一样的,并由程序运行读入, 若读入迷宫大小的值是n(3<n<=10),则该迷宫横向或纵向尺寸都是n,规定迷宫最外面的一圈是障碍物,迷宫的入口是maze[1][1],出口是maze[n-2][n-2], 若maze[i][j] = 1代表该位置是障碍物,若maze[i][j] = 0代表该位置是可以行走的空位(0<=i<=n-1, 0<=j<=n-1)。求从入口maze[1][1]到出口maze[n-2][n-2]可以走通的路径上经历的最短的总步长。要求迷宫中只允许在水平或上下四个方向的空位上行走,走过的位置不能重复走。
输入格式:
输入迷宫大小的整数n, 以及n行和n列的二维数组(数组元素1代表障碍物,0代表空位)
输出格式:
若有可行的通道则输出一个整数,代表求出的通道的最短步长;若没有通道则输出"No solution"
输入样例:
10
1 1 1 1 1 1 1 1 1 1
1 0 0 1 0 0 0 1 0 1
1 0 0 1 0 0 0 1 0 1
1 0 0 0 0 1 1 0 0 1
1 0 1 1 1 0 0 0 0 1
1 0 0 0 1 0 0 0 0 1
1 0 1 0 0 0 1 0 0 1
1 0 1 1 1 0 1 1 0 1
1 1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1
上述输入代表的是如下这样一个迷宫:
其中红色的小方块是障碍物,蓝色的小方块是空位,白色的小圆连起来是一条从入口到出口的通道,两个圆之间代表一个步长。
输出样例:
14
预习作业:
- 数组指针:是一个指向数组的指针
int a[100],*p;
p=&a[0];- 指针数组:指针数组是以指针定义的指针类型数组
int *p[n];- 指针函数:是带指针的函数,即本质是一个函数,(摘录:指针函数是指带指针的函数,即本质是一个函数。函数返回类型是某一类型的指针
类型标识符 *函数名(参数表)
int *f(x,y);
1
2
3
首先它是一个函数,只不过这个函数的返回值是一个地址值。函数返回值必须用同类型的指针变量来接受,也就是说,指针函数一定有函数返回值,而且,在主调函数中,函数返回值必须赋给同类型的指针变量。
表示:
float *fun();
float *p;
p = fun(a);
注意指针函数与函数指针表示方法的不同,千万不要混淆。最简单的辨别方式就是看函数名前面的指针*号有没有被括号()包含,如果被包含就是函数指针,反之则是指针函数)
- 函数指针:是指向函数的指针变量,本质是一个指针变量;
(摘录:int (f) (int x); / 声明一个函数指针 */
f=func; /* 将func函数的首地址赋给指针f */
指向函数的指针包含了函数的地址,可以通过它来调用函数。声明格式如下:
类型说明符 (函数名)(参数)
其实这里不能称为函数名,应该叫做指针的变量名。这个特殊的指针指向一个返回整型值的函数。指针的声明笔削和它指向函数的声明保持一致。
指针名和指针运算符外面的括号改变了默认的运算符优先级。如果没有圆括号,就变成了一个返回整型指针的函数的原型声明。
例如:
void (fptr)();
把函数的地址赋值给函数指针,可以采用下面两种形式:
fptr=&Function;
fptr=Function;
取地址运算符&不是必需的,因为单单一个函数标识符就标号表示了它的地址,如果是函数调用,还必须包含一个圆括号括起来的参数表。
可以采用如下两种方式来通过指针调用函数:
x=(*fptr)();
x=fptr())
- 二级指针:A(即B的地址)是指向指针的指针,就是在给定的指针基础上再将上一个指针值存放到一个新的指针里面;
int main(int a, char **p)
这些也不会做