cf1294E

题意简述：给一个矩阵，有两种操作可以进行

操作1：改变矩阵中一个元素的值

操作2：将矩阵中某一列的值循环下移

要求用最少的操作次数使得矩阵变成

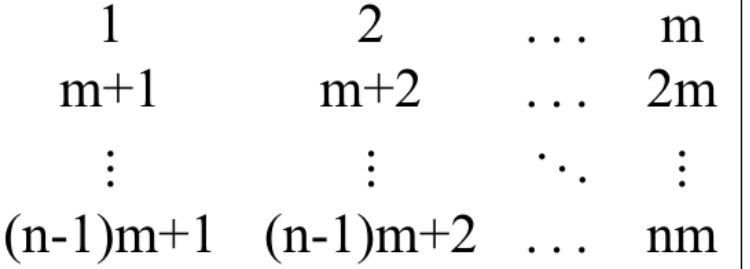
题解：对于一列来说，我们肯定是先变化然后再循环下移，所以应该考虑变化哪些数字，而要知道变化哪些数字必须知道变化之后对应哪个循环，

比如3 1 4 ，可以变为 1 4 7 ， 4 7 1 ， 7 1 4 这三种，我们可以枚举他变成哪一种，然后计算需要的最少操作次数，这样明显会超时

反过来考虑，对于每一个元素来说，找他对哪几种最终的循环有贡献，也就说变成这种循环，他的值不需要改变，可以用dp[i]来表第i种循环，循环扫描每一个元素，更新dp数组就好

#include<bits/stdc++.h>
#define forn(i, n) for (int i = 0 ; i < int(n) ; i++)
#define fore(i, s, t) for (int i = s ; i < (int)t ; i++)
#define fi first
#define se second
#define all(x) x.begin(),x.end()
#define pf2(x,y) printf("%d %d
",x,y)
#define pf(x) printf("%d
",x)
#define each(x) for(auto it:x)  cout<<it<<endl;
#define pii pair<int,int>
using namespace std;
typedef long long ll;
const int maxn=4e5+5;
const int maxm=2e5+5;
const int inf=1e9;

int n,m;

vector<vector<int>> a;

int dp[maxn];

int calc(vector<int> v,int col){
	for(int i=0;i<n;i++)
		dp[i]=0;
	for(int i=0;i<v.size();i++){
		int x=(v[i]-col)/m,y=v[i]%m==0?m:v[i]%m;
		//cout<<x<<' '<<y<<endl;
		if(y==col) {
			if(x>=i) dp[x-i]++;
			dp[x+n-i]++;
		}
	}
	int re=1e9;
	for(int i=0;i<n;i++)
		re=min(re,(n-dp[i])+(n-i)%n);
//	pf(re);
	return re;
}	
int main(){
	cin>>n>>m;
	a.resize(n,vector<int>(m,0));
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			scanf("%d",&a[i][j]);
	int ans=0;
	for(int i=0;i<m;i++){
		vector<int> v(n);
		for(int j=0;j<n;j++)
			v[j]=a[j][i];
		ans+=calc(v,i+1);
	}
	pf(ans);
}