算法：二分图最小点覆盖——Konig定理

二分图的最小点覆盖，又是一个二分图中非常经典的问题。

例题

原创例题

题目描述
给定一个二分图，结点个数分别为n,m，边数为e，求二分图最大匹配数。

输入格式
第一行，n, m, e。
第二至(e + 1)行，每行两个正整数u, v，表示u, v有一条连边。

输出格式

第一行，二分图最小点覆盖数。
第二行，输出一种最小点覆盖方案的左侧点集，元素与元素之间用一个空格分开。
第三行，输出一种最小点覆盖方案的右侧点集，元素与元素之间用一个空格分开。

输入输出样例

输入

4 4 7
1 1
1 3
2 2
2 3
2 4
3 2
4 2

输出

3
1 2
2

说明/提示
1 <= n, m <= 1000, 1 <= e <= n * m。

二分图最小点覆盖——Konig定理

先说一下什么叫二分图的最小点覆盖，简而言之就是我们希望用尽可能少的点去使所有的边都被选中，这里解释一下：如果说一条边的任意一个顶点被选中那么这条边也被选中。举个例子。

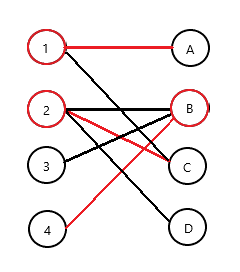
其中的红色边为最大匹配选中的匹配边，红色点为最小点覆盖选中的点，我们可以看到任何一条边都包含一个红点，这就是二分图的最小点覆盖。

现在再来说一下Konig定理：二分图中，最小点覆盖数 = 最大匹配数。

这里我们先来了解一下最小点覆盖的点是如何选择的呢？第一步先做最大匹配，之后我们每次从左边不在匹配边中的一个点开始去按照：未匹配边 -> 匹配边 -> 未匹配边 -> 匹配边 …… 匹配边与未匹配边交替选择的顺序，标记途中经过的顶点，则最后一条经过的边必定为匹配边。这里我开了两个数组vx和vy分别记录每个左侧点是否被标记和每个右侧点是否被标记，上面的例子中3、4、B被标记，但务必牢记最后最小点覆盖的点集并不是这些点组成的集合，而是左侧未被标记的点和右侧被标记的点组成的集合S才是最终答案，例子中为1、2、B。

证明（这里假设选出来的点集为P，最大匹配边的边集为E）：

1. P覆盖了所有边：（反证法）我们假设有一条边左右两端点均不在P集合中，则左端点被标记，右端点未被标记。分类讨论，如果说当前边不在边集E中，则左端点为未被匹配点，又因为当前边不是匹配边，所以必然会从左端点沿当前边开始标记，那么右端点必然被标记，矛盾。如果说当前边在边集E中，其左端点被标记，那么必然是通过右端点链接过来的，则右端点被标记，矛盾。综上，我们可以知道点集P覆盖了所有边。

2. |P| = |E|：我们知道点集P中的左侧点都是匹配点，而右侧点也都为匹配点，又因为一条匹配边上左侧点和右侧点不可能同时在或者不在点集P中，那么E集合中任意一条边左右两端点中都恰好仅有一个点在点集P中，所以|P| = |E|。

3. |P| 是最小的点覆盖数：|P| = 最大匹配数，如果另一个点集的元素个数比|P|更小，那么这个点集必然无法包含所有的匹配边，连所有的匹配边都无法全部包含，怎么可能包含所有边呢。所以|P| 是最小的点覆盖数。

其实求二分图的最小点覆盖数，就是求其二分图的最大匹配数。如果是找最小点覆盖的点的话，就按照上面的思路模拟就行了。

最后，算一下算法时间复杂度：其实就是匈牙利算法的时间复杂度，O(n * m)。

代码

# include <cstdio>
# include <algorithm>
# include <cmath>
# include <cstring>
# include <vector>

using namespace std;

const int N_MAX = 1000, E_MAX = 1000000;

struct Edge
{
	int to, next;
};

int n, m, e;
vector <int> g[N_MAX + 10];

int opp[N_MAX + 10];
bool vis[N_MAX + 10];

bool vx[N_MAX + 10], vy[N_MAX + 10];

void addEdge(int x, int y)
{
	g[x].push_back(y);
}

bool find(int x)
{
	if (vis[x]) return false;
	vis[x] = true;
	for (int i = 0; i < (int) g[x].size(); i++) {
		int y = g[x][i];
		if (opp[y] == 0 || find(opp[y])) {
			opp[y] = x;
			return true;
		}
	}
	return false;
}

void mark(int x)
{
	if (vx[x]) return;
	vx[x] = true;
	for (int i = 0; i < (int) g[x].size(); i++) {
		int y = g[x][i];
		if (opp[y] && !vy[y]) {
			vy[y] = true;
			mark(opp[y]);
		}
	}
}

int hungary()
{
	memset(opp, 0, sizeof(opp));
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		memset(vis, false, sizeof(vis));
		ans += find(i);
	}
	return ans;
}

int konig()
{
	int ans = hungary();
	memset(vis, false, sizeof(vis));
	for (int i = 1; i <= m; i++)
		vis[opp[i]] = true;
	memset(vx, false, sizeof(vx));
	memset(vy, false, sizeof(vy));
	for (int i = 1; i <= n; i++)
		if (!vis[i]) mark(i);
	return ans;
}

int main()
{
	scanf("%d%d%d", &n, &m, &e);
	for (int i = 1; i <= e; i++) {
		int x, y;
		scanf("%d%d", &x, &y);
		addEdge(x, y);
	}
	printf("%d
", konig());
	for (int i = 1; i <= n; i++)
		if (!vx[i]) printf("%d ", i);
	puts("");
	for (int i = 1; i <= m; i++)
		if (vy[i]) printf("%d ", i);
	puts("");
	return 0;
}