大意:给定A数组B数组,从中选择N-K个使得R最大,输出Round(100*R);
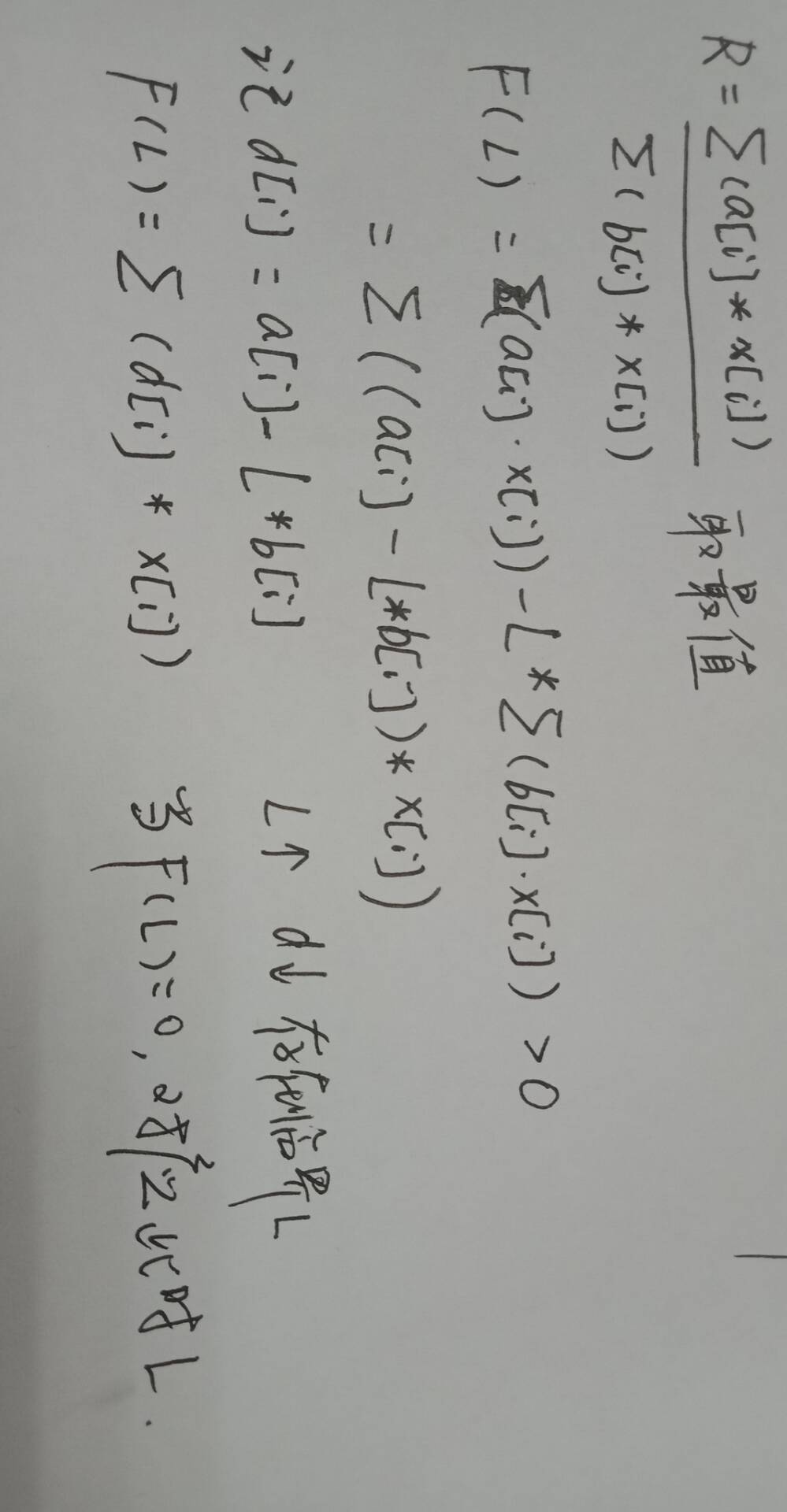

**01分数规划问题思路大抵如此,但是有的题目的限制条件苛刻,题目就变难了。
**分析:限制很简单,只是数目上有所限制,处理方法也很简单,求出D数组后从大到小排列,从先前向后取N-K个即可,这时的D一定是最大的
二分 l 当 F(l) >= 0 时,l = mid,否则,r = mid
/**/
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cctype>
#include <iostream>
#include <algorithm>
#include <map>
#include <set>
#include <vector>
#include <string>
#include <stack>
#include <queue>
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
bool Sqrt(LL n) { return (LL)sqrt(n) * sqrt(n) == n; }
const double PI = acos(-1.0), ESP = 1e-10;
const LL INF = 99999999999999;
const int inf = 999999999, N = 1e3 + 24;
int n, k, a[N], b[N];
double d[N];
bool check(double rate)
{
for(int i = 0; i < n; i++) d[i] = a[i] - rate * b[i];
sort(d, d + n);
double F = 0;
for(int i = n - 1; i >= k; i--) F += d[i];
return F >= 0;
}
double solve()
{
double l = 0, r = 1, mid = 0;
while(r - l > 1e-6) {
mid = (l + r) / 2;
if(check(mid)) l = mid;
else r = mid;
}
return 100 * mid;
}
int main()
{
//freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
while(~scanf("%d%d", &n, &k) && (n || k)) {
for(int i = 0; i < n; i++) scanf("%d", &a[i]);
for(int i = 0; i < n; i++) scanf("%d", &b[i]);
printf("%.0f
", solve());
}
return 0;
}
/*
input:
output:
modeling:
methods:
complexity:
summary:
*/