基础知识
变量定义
在研究变量关系的过程中,通常对于被研究的变量,称为因变量,也称为被解释变量,一般用Y表示。其它用来说明或解释因变量变化的变量称为自变量,也称为解释变量,用X表示。自变量可以有一个,也可以有多个。例如,如果我们想预测销售收入,则销售收入就是我们这次研究的因变量,如果我们是通过广告费的支出来预测销售收入,则广告费支出就是自变量。如果预测销售收入时,还要考虑销售价格或销售人员的数量的影响,那么,销售价格或销售人员的数量这两个因素也都称为自变量,即有两个自变量。
变量之间的关系
在统计学中,依据变量与变量之间的联系或依存的类型不同,一般将变量之间的关系划分为函数关系和相关关系两种。
1.相关关系
所谓相关关系,是指变量的数值之间存在着非严格的依存关系。就是说,当一个变量或几个变量取定一个数值时,另一个对应变量的数值是不确定的。但是,该变量的数值却是随着前述变量的所取数值而发生一定的变化规律。例如,人的身高与体重之间的关系就属于相关关系。就全社会而言,对于具有同样身高的人,体重的数值未必相同。也就是说,同样的身高数值对应的体重数值是不确定的。但是体重数值却是随着“身高越高,体重越重”这个一般的规律而变化。因此两者是一种相关关系。当给定一个房屋面积时,房屋的出租价格是不确定的。但是,出租价格却是依据房屋面积的大小而变化。
如果变量之间存在相关关系,可能包含以下几种情况:
1、变量之间存在着因果关系。例如,产量与单位成本的相关关系就是一种因果关系,其中产量变动在前是原因,单位成本的变动在后是结果。粮食的产量与施肥量的关系也是一种因果关系,施肥量是原因,产量是结果。
2、变量之间存在着相互依存的关系。例如,一个城市的货运量与该城市的国内生产总值具有相关关系,但在货运量与国内生产总值的变动中,很难确定哪一个是原因哪一个是结果,两个变量之间是相互依存的关系。
3、变量之间只是存在着数值的统计关系,或者说是虚假关系。例如,有人将某段时间的香烟销售量与人口的期望寿命数据进行计算,发现两个变量之间具有正的相关关系:香烟销售量越来越多,人口的期望寿命也越来越高。这种相关关系就是典型的虚假相关。首先要定性分析,只有在科学理论上能够解释变量之间确实有联系,才能认为变量的数值之间存在着相关关系。否则,不能使用这种虚假的相关关系作任何的推测或预测。
在客观现实中,许多现象之间都存在着某种相互联系或相互依存的关系。例如,降雨量与云层厚度之间的关系,居民收入增长率与物价指数的关系,人的身高和体重的关系,汽车行使速度与行使里程之间的关系,圆的面积与圆的半径之间的关系等。现象与现象之间的关系如果使用数量来描述,就形成变量与变量之间的关系。2.
2.函数关系
所谓函数关系,是指各变量之间的数值依一定的函数形式所形成的一一对应关系。也就是说,当一个变量或几个变量取一定的值时,另一个变量有一个确定的值与之相对应。例如,当给出圆的半径r时,就可以根据S=πr2,计算出圆面积S;反之,给定圆的面积S,同样根据S=πr2,可以计算出圆的半径r。因此说,圆面积S与圆半径r是函数关系。类似地,当某种商品的销售价格保持不变时,销售额与销售量也可以看作是函数关系。给定销售量就可以知道销售额,有了销售额就可以知道销售量。变量之间的函数关系在自然科学中是普遍存在的。在数学、物理学和化学中有许多严格的定理和公式,这些定理和公式揭示了变量之间存在的相互关系,冥王星的发现就是万有引力定律的最好应用。
在分析多组数据之间的关系时,首先需要通过相关分析确定数据之间的相关关系,然后再通过回归分析确定数据之间的函数关系。这就引出了相关分析与回归分析。
相关与回归分析关系
在研究因变量时,一方面需要研究哪些变量与因变量相关以及关联程度的强弱,这种研究可以称为相关分析。另一方面需要研究因变量与自变量之间是否具有某种数量关系,确定因变量与自变量之间的数学模型,这种研究称为回归分析。
相关分析与回归分析有着密切的联系,它们不仅具有共同的研究对象,而且基础理论也具有一致性。在对变量研究时经常需要它们相互补充。相关分析要为变量之间建立回归模型提供依据;回归分析揭示出变量相关的具体形式。只有当变量之间存在着高度相关时,进行回归分析才可能是正确的。同理,只有通过回归模型掌握了变量之间关联的具体形式,相关分析才有意义。
虽然相关分析与回归分析经常同时使用,但是,它们在研究目的和方法上还是有着明显区别的。首先,在研究目的上不同。进行相关分析是为了得到变量间的关联程度;二回归分析是为了得到因变量与自变量的关系模型。其次,在进行相关分析时,一般不需要区别因变量和自变量,且两种变量都属于随机变量;而建立回归模型却必须去边因变量和自变量,并且因变量是随机变量,自变量被看作是确定性变量。
那么如何量化变量之间的相关程度?两个变量间线性关系的程度。用相关系数r(-1 —— 1)来描述。
- 正相关:如果x,y变化的方向一致,如身高与体重的关系,r>0;
- 负相关:如果x,y变化的方向相反,如吸烟与肺功能的关系,r<0;
- 无线性相关:r=0。
相关程度根
·|r|>0.95 存在显著性相关;
·|r|≥0.8 高度相关;
·0.5≤|r|<0.8 中度相关;
·0.3≤|r|<0.5 低度相关;
·|r|<0.3 关系极弱,认为不相关。
回归分析
回归分析(regression analysis)通过建立模型来研究变量之间相互关系的密切程度、结构状态及进行模型预测的工具,可以确定两种或两种以上变量间相互依赖的定量关系的一种方法,在机器学习中是重要的一个模块,在sklearn机器学习库中有广泛的算法实现,如OLS,脊回归等,回归分析的研究范围:
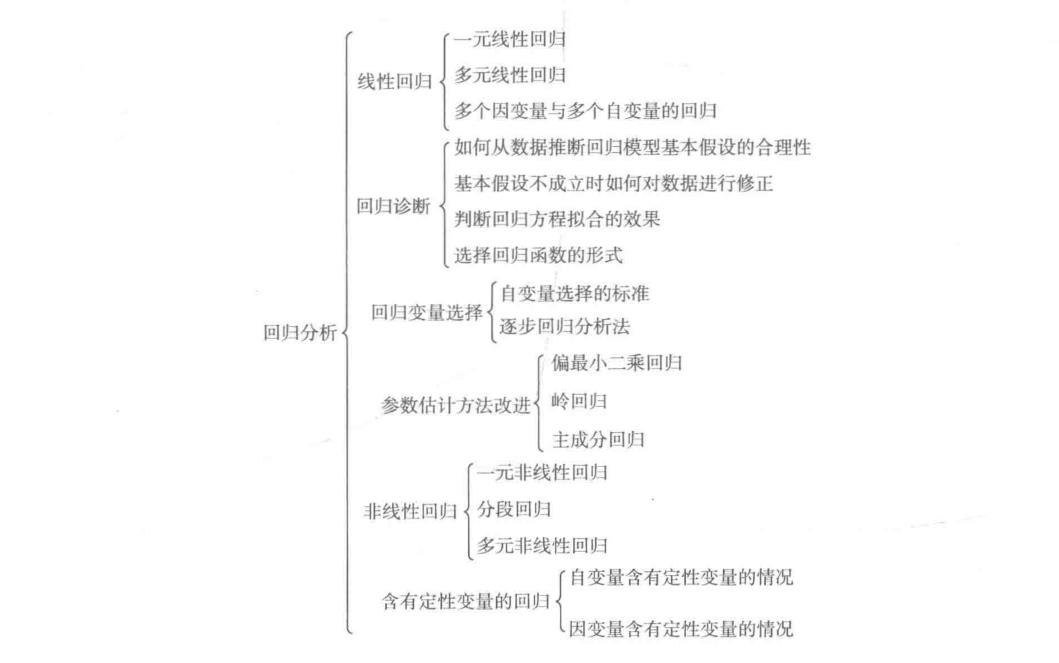
回归分析分类
按变量的多少划分:
如果只研究两个变量之间的相关关系则称为单相关,对这两个变量所做的回归分析叫一元回归,也称为简单回归。其中一个变量是因变量,另一个变量是自变量。当所研究的是一个变量与两个或两个以上变量的相关关系时,称为复相关。对这些变量所作的回归分析就称为多元回归,其中一个变量是因变量,其它变量是自变量。
按相关与回归的形式划分:
当变量之间的关系可以通过线性方程表达时,它们的关系就是线性相关,对此进行的回归分析称为线性回归。反之,称为非线性相关,相应的回归分析称为非线性回归。在只有两个变量时,线性关系体现为直线关系,非线性关系体现为曲线关系。通过散点图可以直接观察变量之间是否具有线性关系。
多重线性回归:
如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关性,此时称为多重线性回归分析。
如果我们要预测的数据模型中,自变量之间存在多重共线性时,那么再使用最小二乘法进行权重参数求解不会准确,消除多重共线性的参数改进估计方法主要有岭回归和主成分回归。
注意:线性回归的入手一般会根据最小二乘法,但是如果结果不好的话,要考虑多变量之间是否存在多重线性相关性。
常见的回归模型:
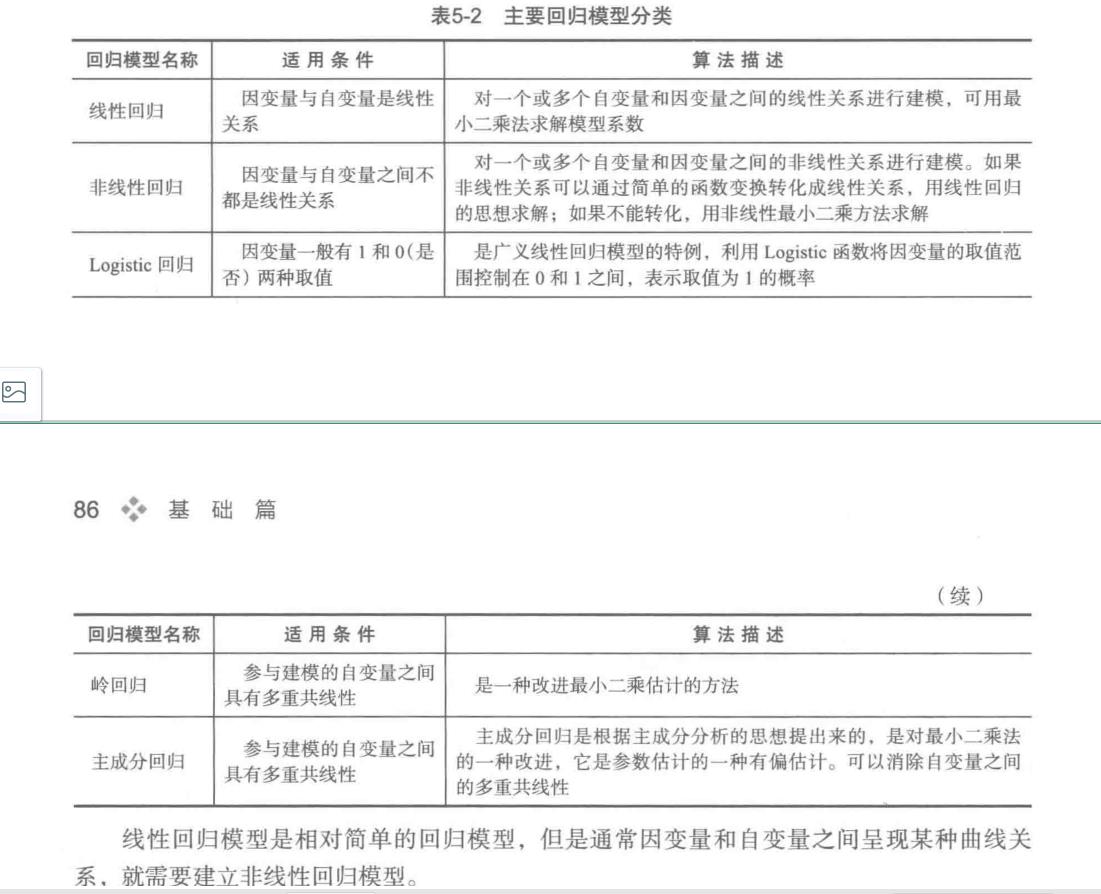
参考:
Python数据分析与挖掘实战