qbxt Day 2 morning
——2020.1.18 济南 主讲:李佳实
目录一览
1.并查集
2.堆
总知识点:基础数据结构
一、并查集
1.描述:并查集是一类十分常用的数据类型,它有着十分广泛的应用。在信息竞赛中,它主要执行的操作一般有三种。
(1) 合并a,b两个元素所在的集合 Merge(a,b)
(2)查找某个元素属于哪个集合 find(k)
(3)查询两个元素是否属于同一集合 Query(a,b)
2.函数模板
(1)find
int find(int x){
if(fa[x]==x) return x; //找到即返回
int t=find(fa[x]); //继续递归find
return t;
}
(2)Merge
void merge(int x,int y){
x=find(x);
y=find(y);
if(x==y) return; //根相同,无需合并,即返回
fa[x]=y; //根不同,即合并
}
3.对于find和merge的优化
(1)
对于merge:启发式合并(使用次数少)
描述:在合并集合S1、S2的时候,我们让较小的树成为较大的树的子树。这里可以是深度、节点个数等启发函数来比较树的大小(一般使用深度)。
代码实现会使用到并查集,而且并不常用,暂且略。
(2)
对于find:路径压缩(常用,效率高,代码简单)
描述:我们在查找完u至根节点的路径之后,一般将这条路径上的所有节点的父节点都设为根节点,这样可以大大减少之后的查找次数。
代码;
int find(int x){
if(fa[x]==x) return x;
int t=find(fa[x]);
fa[x]=t; //记录路径上的节点成为父节点,减少查询次数
return t;
}
(3)时间复杂度分析:
可以证明,经过启发式合并和路径压缩之后的并查集,执行m次查找的复杂度为O(mα(m))
注α(m):Ackermann函数的某个反函数,可以近似的认为它是小于5的。所以并查集的单次查找操作的时间复杂度也几乎是常数级的。
4.例题:
(1)[Noi2015]程序自动分析
题目描述:
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设x1,x2,x3,…代表程序中出现的变量,给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为:x1=x2,x2=x3,x3=x4,x1≠x4,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
注:1≤n≤1000000
样例:

分析:这个题核心思想就是:看输入的是1,我们把它加到一个并查集里去,是0,我们暂且不管。操作好以后,我们特判是0,但树根相同的这种情况,显然是不成立的。标记下来,一个个输出就结束了。
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define N 1000010
using namespace std;
int fa[N];
int find(int x) //寻找函数
{
if(fa[x]==x) return x;
int t=find(fa[x]);
fa[x]=t;
return t;
//return fa[x]==x?x:fa[x]=find(fa[x]);
}
void merge(int x,int y) // 合并函数
{
x=find(x);
y=find(y);
if(x==y) return;
fa[x]=y;
}
int m,x[N],y[N],f[N];
void doit()
{
memset(fa,0,sizeof(fa)); //记得清空
for(int i=1;i<=1000000;i++) fa[i]=i; //初始化
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>x[i]>>y[i]>>f[i];
if(f[i]==1) merge(x[i],y[i]); // 合并
}
bool ans=true;
for(int i=1;i<=m;i++)
{
if(f[i]==0)
{
if(find(x[i])==find(y[i])) ans=false; //如果在一个并查集里,但不是1,那就显然不成立,进行标记
}
}
puts(ans?"YES":"NO");
}
int main()
{
int T;
cin>>T;
while(T--) doit();
}
二、堆
1.描述:堆的物理结构就是数组,堆的逻辑结构是一棵完全二叉树。树中每个结点与数组中存放该结点中值的那个元素相对应。如下图:
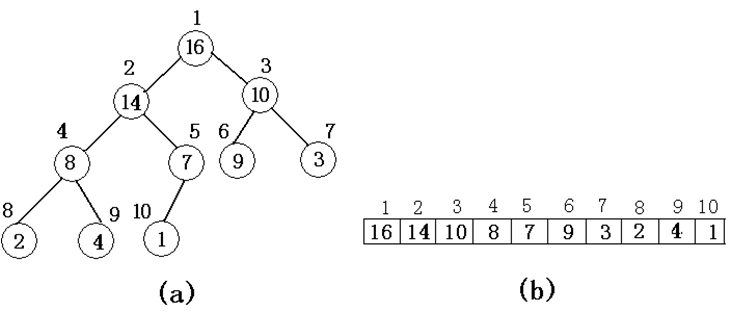
2.性质
(1)若节点x的两儿子为y,z,且x的编号为i。则y(左儿子)为2i,z(右儿子)为2i+1。
(2)对于大顶堆(小顶堆对称考虑)来说(根节点是全局最大值),每个节点的值都大于等于它的儿子节点的值。
3.基本操作
(1)up(即上浮操作)
思想:当小根堆的元素值h[x]变小时,该结点可能会上浮,如果h[x]小于h[x /2]则交换两个结点的值,如此循环下去直到x = 1或h[x] ≥ h[x /2]。
代码:
void up(int x){
while(x>1){
int y=x/2; //x的左儿子
if(a[y]>a[x]){ //比较编号
swap(a[x],a[y]);
x=y; //直接覆盖
}
else break;
}
}
(2)down(即下沉操作)
思想:当小根堆的元素值h[x]变大时,该结点可能会下沉,如果有儿子结点值小于该结点的值则跟较小儿子结点交换,如此循环下去直到条件不满足或者没有儿子结点。
代码:
void down(int x){
while(x*2<=n){
int y=x*2;
if(x*2+1>n){ //不确定右儿子的有无,需判断
//这里为没有右儿子
if(a[y]<a[x]){
swap(a[x],a[y]);
x=y;
}
else break;
}
else{ //有右儿子
int z=y+1; //右儿子编号为2i+1,左儿子为2i,右儿子=左儿子+1
if(a[y]<a[z]){
if(a[y]<a[x]){
swap(a[x],a[y]);
x=y;
}
else break;
}
else{
if(a[z]<a[x]){
swap(a[x],a[z]);
x=z;
}
else break;
}
}
}
}
(3)insert(即插入操作)
思想:插入一个元素,把该元素放在最后,再做up操作。
代码:
void insert(int x){
a[++n]=x;
up(n);
}
(4)delete(即删除操作)
思想:删除第x个元素,为了不破坏堆的性质,把h[len]移到x处,堆元素个数len减一,再判断做up(x)还是down(x)。
代码:
void del(int x){
a[x]=a[n]; //放
n--; //减空间
//判断up还是down
if(x!=1&&a[x]<a[x/2]) up(x);
else down(x);
}
4.例题
(1)堆排序
题目描述:使用堆完成n个整数的排序操作
分析:先用build把输入数组A[1…n]建成一个大根堆。因为数组中最大元素在根A[1],可以通过把它与A[n]互换来达到最终正确的位置,然后把堆的元素个数减1,再通过down(1)操作把剩下的n - 1个元素调整成大根堆,如此反复执行n - 1次。(O(nlogn))
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define N 1000010
using namespace std;
int n,a[N];
void up(int x)
{
while(x>1)
{
int y=x/2;
if(a[y]>a[x])
{
swap(a[x],a[y]);
x=y;
}
else break;
}
}
void down(int x)
{
while(x*2<=n)
{
int y=x*2;
if(x*2+1>n)
{
if(a[y]<a[x])
{
swap(a[x],a[y]);
x=y;
}
else break;
}
else
{
int z=y+1;
if(a[y]<a[z])
{
if(a[y]<a[x])
{
swap(a[x],a[y]);
x=y;
}
else break;
}
else
{
if(a[z]<a[x])
{
swap(a[x],a[z]);
x=z;
}
else break;
}
}
}
}
void insert(int x){
a[++n]=x;
up(n);
}
void del(int x){
a[x]=a[n];
n--;
if(x!=1&&a[x]<a[x/2]) up(x);
else down(x);
}
void build() //建堆
{
for(int i=n/2;i;i--) down(i);
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
build();
int m=n; //提前记录n值,因为这个值会被后面的操作改变
for(int i=1;i<=m;i++)
{
int x=a[1];
del(1); //删堆顶
cout<<x<<' ';
}
cout<<endl;
}