Consider some square matrix A with side n consisting of zeros and ones. There are n rows numbered from 1 to n from top to bottom and n columns numbered from 1 to n from left to right in this matrix. We'll denote the element of the matrix which is located at the intersection of the i-row and the j-th column as Ai, j.
Let's call matrix A clear if no two cells containing ones have a common side.
Let's call matrix A symmetrical if it matches the matrices formed from it by a horizontal and/or a vertical reflection. Formally, for each pair (i, j) (1 ≤ i, j ≤ n) both of the following conditions must be met: Ai, j = An - i + 1, j and Ai, j = Ai, n - j + 1.
Let's define the sharpness of matrix A as the number of ones in it.
Given integer x, your task is to find the smallest positive integer n such that there exists a clear symmetrical matrix A with side n and sharpness x.
The only line contains a single integer x (1 ≤ x ≤ 100) — the required sharpness of the matrix.
Print a single number — the sought value of n.
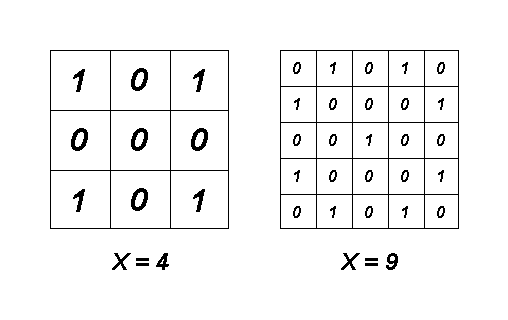
4
3
9

1 #include<cstdio> 2 3 const int MAXN=105; 4 5 int a[MAXN]; 6 7 int main() 8 { 9 a[1]=1; 10 a[3]=5; 11 a[2]=a[4]=a[5]=3; 12 for(int i=5;i<MAXN;) 13 { 14 int x=(a[i]+1)*2; 15 for(int j=i+1;j<=i+x;j++) 16 a[j]=a[i]+2; 17 i+=x; 18 } 19 20 int x; 21 while(scanf("%d",&x)!=EOF) 22 { 23 printf("%d ",a[x]); 24 } 25 26 return 0; 27 28 }
The figure below shows the matrices that correspond to the samples: