Codeforces Round #283 (Div. 2) 题解

 

　　　　　　　　A. Minimum Difficulty

 

Mike is trying rock climbing but he is awful at it.

There are n holds on the wall, i-th hold is at height ai off the ground. Besides, let the sequence ai increase, that is, ai < ai + 1 for all ifrom 1 to n - 1; we will call such sequence a track. Mike thinks that the track a1, ..., an has difficulty 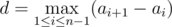. In other words, difficulty equals the maximum distance between two holds that are adjacent in height.

Today Mike decided to cover the track with holds hanging on heights a1, ..., an. To make the problem harder, Mike decided to remove one hold, that is, remove one element of the sequence (for example, if we take the sequence (1, 2, 3, 4, 5) and remove the third element from it, we obtain the sequence (1, 2, 4, 5)). However, as Mike is awful at climbing, he wants the final difficulty (i.e. the maximum difference of heights between adjacent holds after removing the hold) to be as small as possible among all possible options of removing a hold. The first and last holds must stay at their positions.

Help Mike determine the minimum difficulty of the track after removing one hold.

Input

The first line contains a single integer n (3 ≤ n ≤ 100) — the number of holds.

The next line contains n space-separated integers ai (1 ≤ ai ≤ 1000), where ai is the height where the hold number i hangs. The sequence ai is increasing (i.e. each element except for the first one is strictly larger than the previous one).

Output

Print a single number — the minimum difficulty of the track after removing a single hold.

Sample test(s)

input

3
1 4 6

output

5

input

5
1 2 3 4 5

output

2

input

5
1 2 3 7 8

output

4


意思：一个非递增的数组，定义这个数组的难度为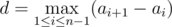
　　　现在要从这个数组中拿掉一个数（必须拿掉），问拿掉哪个数使得这个数组的难度最小。


思路：记录这个数组（数组本身不用记录）两两的距离，然后找出a[i]+a[i+1]的最小值，就是去掉中间这个数了，再用这个a[i]+a[i+1]和数组原来的难度相比，大的那个就是ans了。

#include<cstdio>
const int maxn=104;
int a[maxn];
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        int pre,p;
        int tot=1;
        scanf("%d",&pre);
        for(int i=2;i<=n;i++)
        {
            scanf("%d",&p);
            a[tot++]=p-pre;
            pre=p;
        }
        int ans=100000;
        for(int i=1;i<tot-1;i++)
        {
            if(a[i]+a[i+1]<ans)
                ans=a[i]+a[i+1];
        }
        for(int i=1;i<tot;i++)
        {
            if(a[i]>ans)
                ans=a[i];
        }
        printf("%d
",ans);
    }
    return 0;
}

            　　　　　　　　  C. Removing Columns

You are given an n × m rectangular table consisting of lower case English letters. In one operation you can completely remove one column from the table. The remaining parts are combined forming a new table. For example, after removing the second column from the table

abcd
edfg
hijk

 

we obtain the table:

acd
efg
hjk

 

A table is called good if its rows are ordered from top to bottom lexicographically, i.e. each row is lexicographically no larger than the following one. Determine the minimum number of operations of removing a column needed to make a given table good.

Input

The first line contains two integers  — n and m (1 ≤ n, m ≤ 100).

Next n lines contain m small English letters each — the characters of the table.

Output

Print a single number — the minimum number of columns that you need to remove in order to make the table good.

Sample test(s)

input

1 10
codeforces

output

0

input

4 4
case
care
test
code

output

2

input

5 4
code
forc
esco
defo
rces

output

4

题意：给出一个n*m的矩阵，上面放着小写字符。

要求：删除其中的一些列，使得矩阵从上到下，每一行组成的字符串的字典序由小到大（可以相等）

思路：
从第1列->第m列：考虑是否要去掉，去掉则把字符标记为‘A'。

#include<cstdio>
const int maxn=110;
char a[maxn][maxn];
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        char str[maxn];
        for(int i=1;i<=n;i++)
        {
            scanf("%s",&str);
            for(int j=1;j<=m;j++)
            {
                a[i][j]=str[j-1];
            }
        }
        if(n==1)
        {
            printf("0
");
            continue;
        }
        int ans=0;
        for(int j=1;j<=m;j++)
        {
            for(int i=2;i<=n;i++)
            {
                int u=a[i][j];
                int v=a[i-1][j];
                if(u<v)
                {
                    int w=1;
                    while(a[i][w]==a[i-1][w]||a[i][w]=='A')
                        w++;
                    if(w==j)
                    {
                        ans++;
                        //刚开始这里写成t=n，当然无限循环了，然后输入数据后
                        //一直没有输出结果，我甚至开始怀疑人生了
                        //检查了一个小时，呵呵
                        for(int t=1;t<=n;t++)
                        {
                            a[t][j]='A';
                        }
                        break;
                    }
                }
            }
        }
        printf("%d
",ans);
    }
    return 0;
}

　　　　　　　　　　B. Secret Combination

You got a box with a combination lock. The lock has a display showing n digits. There are two buttons on the box, each button changes digits on the display. You have quickly discovered that the first button adds 1 to all the digits (all digits 9 become digits 0), and the second button shifts all the digits on the display one position to the right (the last digit becomes the first one). For example, if the display is currently showing number 579, then if we push the first button, the display will show 680, and if after that we push the second button, the display will show 068.

You know that the lock will open if the display is showing the smallest possible number that can be obtained by pushing the buttons in some order. The leading zeros are ignored while comparing numbers. Now your task is to find the desired number.

Input

The first line contains a single integer n (1 ≤ n ≤ 1000) — the number of digits on the display.

The second line contains n digits — the initial state of the display.

Output

Print a single line containing n digits — the desired state of the display containing the smallest possible number.

Sample test(s)

input

3
579

output

024

input

4
2014

output

0142

题意：有一个串数字，现在你可以有2种操作：
1.把这串数字的每个数字加1 (随便你做多少次)
2.把这串数字的最后一个数字放到最前面，其余的后移一位(随便多少次都可以)
问：这串数字经过你的操作后，可能出现的最小数字是多少。

思路：刚开始看到这道题，我觉得是很难的，一想，其实很简单。
数字最小,则操作后，第一位一定是0
先操作1，则出现0的位置一共有n<=1000种可能，然后操作2，把0放到最前面。
当然，也可以先不断调整首位的数字，再把第一位的数字变为0.(我的代码也是这样)

#include<cstdio>
const int maxn=1010;
char a[maxn];       //输入的数字串
int b[maxn];        //首位为0时的数字串
int ans[maxn];     //存储当前的最小值
int n;
void update()
{
    bool flag=false;
    for(int i=0;i<n;i++)
    {
        if(b[i]>ans[i])        //说明b>ans了，后面的不用再比较了，开始没有这一步，wa了
            break;
        if(b[i]<ans[i])
        {
            flag=true;
            break;
        }
    }
    if(flag)
    {
        for(int i=0;i<n;i++)
            ans[i]=b[i];
    }
}
int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        scanf("%s",&a);
        for(int i=0;i<n;i++)     //初始化ans为99999999......
            ans[i]=9;
        for(int i=0;i<n;i++)     //n次
        {
                                    //m表示首位加多少个1变成0
            int m=10-(a[0]-'0');   //-'0'和+'0'是不一样的
            for(int j=0;j<n;j++)
            {
                int u=a[j]-'0';
                b[j]=(u+m)%10;     //%10
            }
            update();              //更新ans
            char p=a[n-1];      
            for(int j=n-1;j>0;j--)   //执行操作2，调整首位的数字
                a[j]=a[j-1];         //注意，这里要从后往前，不能从前往后
            a[0]=p;
        }
        for(int i=0;i<n;i++)
            printf("%d",ans[i]);
        printf("
");
    }
    return 0;
}