Description
欢乐岛上有个非常好玩的游戏,叫做“紧急集合”。在岛上分散有N个等待点,有N-1条道路连接着它们,每一条道路都连接某两个等待点,且通过这些道路可以走遍所有的等待点,通过道路从一个点到另一个点要花费一个游戏币。
参加游戏的人三人一组,开始的时候,所有人员均任意分散在各个等待点上(每个点同时允许多个人等待),每个人均带有足够多的游戏币(用于支付使用道路的花费)、地图(标明等待点之间道路连接的情况)以及对话机(用于和同组的成员联系)。当集合号吹响后,每组成员之间迅速联系,了解到自己组所有成员所在的等待点后,迅速在N个等待点中确定一个集结点,组内所有成员将在该集合点集合,集合所用花费最少的组将是游戏的赢家。
小可可和他的朋友邀请你一起参加这个游戏,由你来选择集合点,聪明的你能够完成这个任务,帮助小可可赢得游戏吗?
Input
第一行两个正整数N和M(N<=500000,M<=500000),之间用一个空格隔开。分别表示等待点的个数(等待点也从1到N进行编号)和获奖所需要完成集合的次数。 随后有N-1行,每行用两个正整数A和B,之间用一个空格隔开,表示编号为A和编号为B的等待点之间有一条路。 接着还有M行,每行用三个正整数表示某次集合前小可可、小可可的朋友以及你所在等待点的编号。
Output
一共有M行,每行两个数P,C,用一个空格隔开。其中第i行表示第i次集合点选择在编号为P的等待点,集合总共的花费是C个游戏币。
我天,这题恶心坏了.
话说没出样例就敢交题的我实在是tql。 ~w~
明显到(LCA)处就能取到最小的值。
会需要求到(6)种(貌似可以求的更少.
首先这六种情况怎么算出来的.
其中(C_3^2)代表在三个点中,随便选两个点求(LCA)记作(X)。
然后再求第三个点与(X)的(LCA)记作(Y)
注意,这里要选择(X)作为集合点.这样会更优.
因为走到(Y)的话就会是两个点对花费的贡献.这样明显更大啊.
而走到(X),这两个点对花费的贡献就会比较小了,另一个人多走就好了.
但是感觉不太对.但又的确是对的 emmm
比如这样:
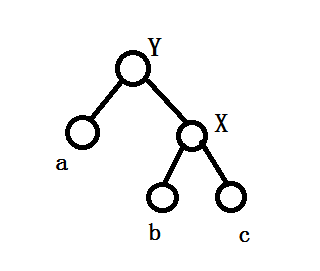
简单来看的话,我们求出了(b)和(c)的(LCA=X)
(a)和(X)的(LCA=Y)
此时(a,b,c)走到(X)的价值为(4),走到(Y)的价值为(5)
(这只是一个小栗子啦 qwq)
代码
#include<cstdio>
#include<cctype>
#include<algorithm>
#define R register
#define N 500008
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int head[N],tot,depth[N],dis[N];
int n,m,gw[N][21],f[N][21];
struct cod{int u,v;}edge[N<<2];
inline void add(int x,int y,int z)
{
edge[++tot].u=head[x];
edge[tot].v=y;
head[x]=tot;
}
void dfs(int u,int fa)
{
f[u][0]=fa;depth[u]=depth[fa]+1;
dis[u]=dis[fa]+1;
for(R int i=1;(1<<i)<=depth[u];i++)
f[u][i]=f[f[u][i-1]][i-1];
for(R int i=head[u];i;i=edge[i].u)
{
if(edge[i].v==fa)continue;
dfs(edge[i].v,u);
}
}
inline int lca(int x,int y)
{
if(depth[x]>depth[y])swap(x,y);
for(R int i=17;i>=0;i--)
if(depth[x]+(1<<i)<=depth[y])
y=f[y][i];
if(x==y)return y;
for(R int i=17;i>=0;i--)
{
if(f[x][i]==f[y][i])continue;
x=f[x][i],y=f[y][i];
}
return f[x][0];
}
int main()
{
in(n),in(m);
for(R int i=1,x,y;i<n;i++)
in(x),in(y),add(x,y,1),add(y,x,1);
dfs(1,0);
for(R int i=1,x,y,z;i<=m;i++)
{
in(x),in(y),in(z);
R int a=lca(x,y),b=lca(x,z),c=lca(y,z);
R int aa=lca(a,z),bb=lca(y,b),cc=lca(x,c);
R int father,res=214748364;
int ansa=dis[x]+dis[y]-2*dis[a]+dis[a]-2*dis[aa]+dis[z];
int ansb=dis[x]+dis[z]-2*dis[b]+dis[b]-2*dis[bb]+dis[y];
int ansc=dis[y]+dis[z]-2*dis[c]+dis[c]-2*dis[cc]+dis[x];
if(res>ansa)res=ansa,father=a;
if(res>ansb)res=ansb,father=b;
if(res>ansc)res=ansc,father=c;
printf("%d %d
",father,res);
}
}