题意：n个点n-1条边；定义集合{A,B,C}若三点能被一条路径覆盖则叫做能被简单路覆盖；求不被简单路覆盖的集合数；
正式做的时候我们队一直在说，树形DP，树形DP。树形DP！
可是三个人都不会= =。。。
思路：由于直接计算情况较多，可转化为算补集，即能被简单路覆盖的集合数。
显然，假设ABC依次为路径上的点，那么A C一定在以B为根的不同子树中。
那么我们就可以通过枚举B 为根，方案数就是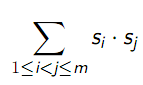
s为B子树的大小；
1 #include <algorithm> 2 #include <iostream> 3 #include <iomanip> 4 #include <cstring> 5 #include <cstdlib> 6 #include <cstdio> 7 #include <string> 8 #include <vector> 9 #include <queue> 10 #include <cmath> 11 #include <stack> 12 #include <map> 13 #include <cmath> 14 #include <set> 15 #include <climits> 16 #define INF 0x7fffffff 17 #define finc(i,a,b) for(i=a;i<=b;i++) 18 #define fdec(i,a,b) for(i=a;i>=b;i--) 19 #define MAXM 100002 20 #pragma comment(linker, "/STACK:16777216") 21 using namespace std; 22 23 const int MAXN = 100010; 24 struct Edge 25 { 26 int to,next; 27 }edge[MAXN*2]; 28 int head[MAXN],tot; 29 void init() 30 { 31 memset(head,-1,sizeof(head)); 32 tot = 0; 33 } 34 void addedge(int u,int v) 35 { 36 edge[tot].to = v; 37 edge[tot].next = head[u]; 38 head[u] = tot++; 39 } 40 int num[MAXN]; 41 int n; 42 long long ans; 43 void dfs(int u,int pre) 44 { 45 num[u] = 1; 46 int tmp = 0; 47 for(int i = head[u];i!= -1;i = edge[i].next) 48 { 49 int v = edge[i].to; 50 if(v == pre)continue; 51 dfs(v,u); 52 ans += (long long)tmp*num[v]; 53 num[u] += num[v]; 54 tmp += num[v]; 55 } 56 ans += (long long)tmp*(n-num[u]); 57 } 58 59 60 int main() 61 { 62 int u,v; 63 while(scanf("%d",&n) == 1) 64 { 65 init(); 66 for(int i = 1;i < n;i++) 67 { 68 scanf("%d%d",&u,&v); 69 addedge(u,v); 70 addedge(v,u); 71 } 72 ans = 0; 73 dfs(1,-1); 74 long long tot = (long long)n*(n-1)*(n-2)/6; 75 printf("%I64d ",tot-ans); 76 } 77 return 0; 78 }