平衡二叉树每一个节点的平衡因子都小于等于1,所以我们判断每一个节点左右子树的深度查是不是小于等于1即可
我们可以从上往下开始判断每一个节点的平衡因子(两个递归,一个求深度,另一个递归树)
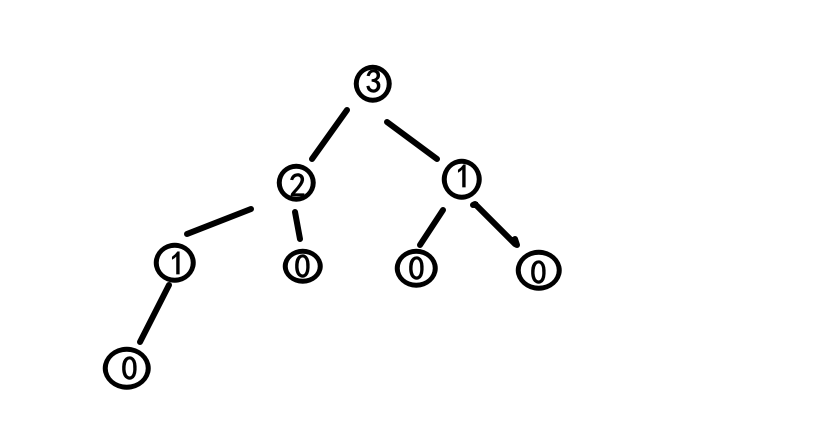
也可以从叶子节点往上递归,把每个节点的深度保存再节点中,判断平衡 因子(下面代码就是使用这种方法)
#include <iostream> #include <vector> #include <algorithm> #include<stack> #include<math.h> #include<string> #include<string.h> #include<map> using namespace std; // Definition for a binary tree node. struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; class Solution { public: //从叶子节点开始往上判断每一个节点的平衡因子 bool isBalanced(TreeNode* root) { if (root == nullptr) { return true; } else { if (isBalanced(root->left) && isBalanced(root->right)) { int left = 0; if (root->left == nullptr) { left = -1; } else { left = root->left->val; } int right = 0; if (root->right == nullptr) { right = -1; } else { right = root->right->val; } if (abs(left - right) < 2) { root->val = left > right ? left + 1 : right + 1;//取较深的值 return true; } else { return false; } } else { return false; } } } }; TreeNode* insert(TreeNode* root, int x) { if (root == NULL) { TreeNode* temp = new TreeNode(0); temp->val = x; temp->left = NULL; temp->right = NULL; return temp; } if(x<root->val) root->left = insert(root->left, x); else root->right = insert(root->right, x); return root; } void Print(TreeNode* root) { if (root == NULL) return; Print(root->left); Print(root->right); cout << root->val << endl; } int main() { TreeNode* root = NULL; int n, x; cin >> n; for (int i = 0; i < n; i++) { cin >> x; root = insert(root, x); } Solution A; cout << A.isBalanced(root) << endl; Print(root); return 0; }