一、什么是最大流问题
简单来说,就是在有向网络图中,单位时间内,从开始点到结束点能通过的最大流量
许多应用都包含了流量问题,例如,公路系统中有车辆流,控制系统中有信息流,供水系统中有水流,金融系统中有现金流等等
二、简单概念
1、源点:出发点。
2、汇点:结束点。
3、流:就是一条可以从源点到汇点的一条合法路径。
4、容量:每条边都有一个容量(水管的最大水流容量)
5、流量:就是一条可以从源点到汇点的一条合法路径能通过的最大数量,大小取决于这条路径上的最小容量
6、增广路:也就是流,一条可以从源点到汇点的一条合法路径
7、残量:就是剩余容量,对于一条边来说,残量=容量-流量
三、求最大流的过程
下图是一个交通运输网络,有1到6共6个结点,两个结点间的数字代表它们之间的最大运输能力,求结点1到结点6在单位时间内的最大运输能力(流量)?

可以看到结点1到结点6之间有多条路径,而所有路径的最大流量之和正是所要求的最大流量,问题转化为求每条路径的最大流量,以路径:1-3-5-6为例,结点间的运输流量分别是10、14、21,容易想到10是这条路径的瓶颈,所以1-3-5-6的最大运行能力是10。同时也意味着,当1-3之间达到运输瓶颈10时,1-3这条路就不再具备运输能力了(就可以把1-3条路从图中去掉了,同时也要把3-5-6路径上的运输能力减掉10,因为已经被我们找到的第一条路径给占用了10,这样就有了下图),记录下第一条路径的最大流量10。

下面继续找一条路径:1-2-5-6,它的剩余最大流量是6。按照上面的方法去掉1-2,并把2-5-6的运输能力减6,就有了下图:

接下来是:1-4-6,它的剩余最大流量是5。

接下来是:1-4-3-5-6,它的剩余最大流量是1。
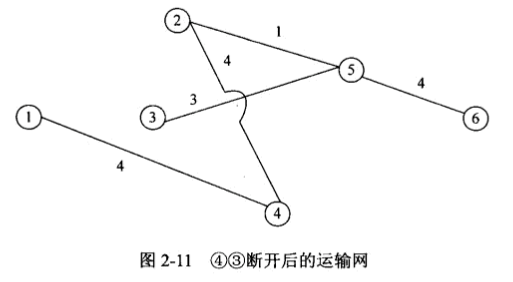
接下来是:1-4-2-5-6,它的剩余最大流量是1。

至此结点1到6之间已经没有通路了,把各个路径的最大流量和加起来即是所求:10+6+5+1+1=23
以上转载自:https://www.jianshu.com/p/e4548c5c381e
反向边的概念
四、代码实现(EK算法)
时间复杂度:O(n*m2),m是边数,n是顶点数量
注意:在读入边的时候,要注意重边的情况,要用加法存边
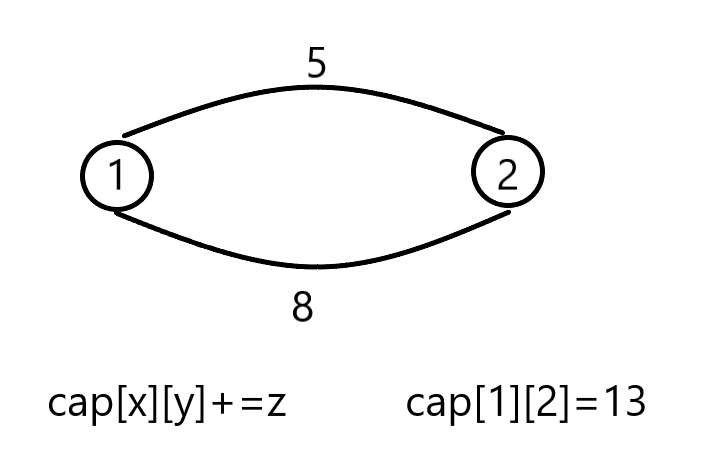
大佬的模板
const int MAXN = 500; const int INF = 0x3fffffff; int cap[MAXN][MAXN];//存边的容量,没有边的初始化为0 int path[MAXN], flow[MAXN]; int n;//点的个数,编号[0,n],包括了源点和汇点。 int st, endd;//源点和汇点 queue<int>p;//队列放外面时间是262ms,放进函数里面去之后就322ms,不懂 int bfs() { while(!p.empty()) p.pop(); memset(path, -1, sizeof(path));//每次搜索前都把路径初始化成-1 path[st] = 0; flow[st] = INF;//源点可以有无穷的流流进 p.push(st); while (!p.empty()) { int now = p.front(); p.pop(); if (now == endd) break; for (int i = 0; i <= n; i++)//枚举所有的点,如果点的编号起始点有变化可以改这里 { if (i != st && path[i] == -1 && cap[now][i]) { flow[i] = flow[now] < cap[now][i] ? flow[now] : cap[now][i]; p.push(i); path[i] = now; } } } if (path[endd] == -1)//即找不到汇点上去了。找不到增广路径了 return -1; return flow[endd]; } int Edmonds_Karp() { int mx_flow = 0; int step, pos, pre; while ((step = bfs()) != -1)//step是残量 { mx_flow += step; pos = endd;//从汇点开始更新流量 while (pos != st) { pre = path[pos]; cap[pre][pos] -= step; cap[pos][pre] += step; pos = pre; } } return mx_flow; }
下面这份模板用起来适用性感觉不是很强,注意使用吧

int flow[205][205],cap[205][205];//flow当前流量,cap总容量 int f[205],vis[205];//f[i]最小残量=cap-flow,vis[i]标记i节点的上一个最小残量所在的位置 int mx_flow;//最大流量,所有增广路最小残量之和 void bfs(int n)//顶点数 { queue<int>p; mx_flow=0; int flag=0; memset(flow,0,sizeof(flow)); while(flag==0) { memset(f,0,sizeof(f)); memset(vis,0,sizeof(vis)); f[1]=mx,vis[1]=-1;//初始化源点 p.push(1); while(!p.empty())//bfs找增广路 { int now=p.front(); p.pop(); for(int i=1;i<=n;i++) { if(!f[i]&&flow[now][i]<cap[now][i]) { f[i]=min(f[now],cap[now][i]-flow[now][i]);//取最小残量 vis[i]=now; p.push(i); } } } if(f[n]==0)//容量-流量==0,一条增广路寻找结束 flag=1; mx_flow+=f[n]; int pos=n;//从汇点开始更新流量 while(!flag&&pos!=1) { flow[vis[pos]][pos]+=f[n];//正向更新流量 flow[pos][vis[pos]]-=f[n];//反向更新流量 pos=vis[pos]; } } }
