Working Plan 优先队列+贪心

题目链接：http://codeforces.com/gym/101987
题目描述
ICPC manager plans a new project which is to be carried out for n days. In this project, m persons numbered from 1 to m are supposed to work. Each day j (1 ≤ j ≤ n) requires dj persons, and each person i (1 ≤ i ≤ m) wants to work wi days.

To increase the efficiency in performing the project, the following two conditions should be satisfied:
    1.each person works for only consecutive w days when he/she works, and
    2.each person can work again after he/she has a rest for at least h days.
ICPC manager wants to find a working plan to assign the working days for all persons such that the number of working days of each person i (1 ≤ i ≤ m) is equal to wi and the number of persons who work for each day j (1 ≤ j ≤ n) is equal to dj, and above two conditions are also satisfied.

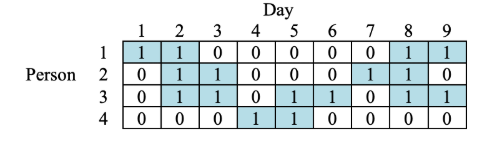
For example, assume the project is carried out for n = 9 days, and m = 4 persons participate in the project. Let w = 2 and h = 1. Also, assume (w1, w2, w3, w4) = (4, 4, 6, 2) and (d1, d2, d3, d4, d5, d6, d7, d8, d9) = (1, 3, 2, 1, 2, 1, 1, 3, 2). The table below shows a feasible solution where the i-th row corresponds to person i, and the j-th column corresponds to day j. If person i works or has a rest in day j, the value of the table element with row i and column j is 1 or 0, respectively.

Given m, n, w, h, wi (1 ≤ i ≤ m) which is a multiple of w, and dj (1 ≤ j ≤ n), write a program to find a feasible solution as a working plan.

输入
Your program is to read from standard input. The input starts with a line containing four integers, m, n, w, h (1 ≤ m ≤ 2,000, 1 ≤ n ≤ 2,000, 1 ≤ w, h ≤ n). The following line contains m integers where the i-th (1 ≤ i ≤ m) integer represents wi (1 ≤ wi ≤ n) which is a multiple of w. The next line contains n integers where the j-th (1 ≤ j ≤ n) integer represents dj (0 ≤ dj ≤ m).

输出
Your program is to write to standard output. If there is a feasible working plan, print 1 in the first line followed by m lines, each i-th (1 ≤ i ≤ m) line should contain wi/w integers. These integers form an increasing sequence of first days that person i works in the feasible plan. If there is no feasible working plan, print only -1 in the first line. The first sample below corresponds to the example given in the table above.

样例输入
样例数据

4 9 2 1
4 4 6 2
1 3 2 1 2 1 1 3 2
样例输出

1
1 8
2 7
2 5 8
4
题意：有m个工人，要工作n天，每个工人可以连续工作w天，之后就要休息h天，给定每个工人的工作天数b[i],和每天需要的工人数a[i],问工人的数量能否满足每天的工作安排，若可以，输出1，并输出每个工人每次开始工作的日期（每个工人的工作次数为b[i]/w），若不能，直接输出-1.

题解：建立两个优先队列，工作队列Q和休息队列T，Q的优先级是工作次数，工作次数越多的越先进入工作队列，T的优先级是休息之后可以开始工作的时间，工作时间越早越先进入队列。工作队列的每个工人工作w天之后进入休息队列，休息队列里记录休息h天之后可以开始工作的日期，若这个日期小于当天日期，就可以进入工作队列

因为每个工人可以连续工作，在用一个vis数组记录每天需要新加入的工人数量

#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
int n, m, w, h;
int a[2005], b[2005], vis[2005];//vis记录每天需要新加入几个工人
vector<int>v[2005];
typedef struct node
{
    int num;//编号
    int cnt;//工作次数
    int time;//休息之后可以开始工作的日期
}node;

typedef struct cmp1//对队列T，可以开始工作的日期越早越先入队列
{
    bool operator () (const node &x, const node &y)
    {
        return x.time > y.time;
    }
}cmp1;
typedef struct cmp2//对队列Q，工作次数越多的越先进入队列
{
    bool operator () (const node &x, const node &y)
    {
        return x.cnt < y.cnt;
    }

}cmp2;
priority_queue<node, vector<node>, cmp2>Q;//工作队列
priority_queue<node, vector<node>, cmp1>T;//休息队列
int main()
{
    node p[2005];
    cin >> m >> n >> w >> h;
    for (int i = 1; i <= m; i++)
    {
        cin >> b[i];
        p[i].num = i;
        p[i].cnt = b[i] / w;
        p[i].time = 0;
        Q.push(p[i]);
    }
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    int flag = 1;
    for (int i = 1; i <= n; i++)
    {
        if(a[i]!=0)
        {
            int temp = a[i];
            vis[i] = a[i];
            for (int j = i; j <= i + w - 1; j++)//因为每个人都是连续工作的，之后的w天都要减去a[i]得到需要新加入的人数
                a[j] = a[j] - temp;
        }
    }
    node temp;
    for (int i = 1; i <= n; i++)
    {
        while (!T.empty())
        {
            temp = T.top();
            if (temp.time <= i)//如果可以开始工作的日期小于当前日期
            {
                Q.push(temp);
                T.pop();
            }
            else
                break;
        }
        while (!Q.empty() && vis[i])
        {
            temp = Q.top();
            Q.pop();
            vis[i]--;
            temp.time = i + w + h;
            temp.cnt--;
            v[temp.num].push_back(i);//记录每次开始工作的日期
                if (temp.cnt != 0)
                    T.push(temp);
        }
        if (vis[i] != 0)//人数不够
        {
            flag = 0;
            break;
        }
    }
    if (flag == 0)
        cout << -1 << endl;
    else
    {
        cout << 1 << endl;
        for (int i = 1; i <= m; i++)
        {
            for (int j = 0; j < v[i].size(); j++)
            {
                cout << v[i][j];
                if (j != v[i].size())
                    cout << ' ';
            }
            cout << endl;
        }
    }
    return 0;

}