数状数组优化DP 之 树状数组处理两个限制条件 之 离散化处理大数据 [BZOJ2131]免费的馅饼

https://blog.csdn.net/Izumi_Hanako/article/details/78276844

首先，DP的关键在于将状态转移方程

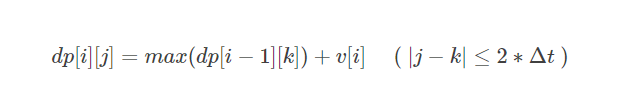
的限制条件简化到一个数据的大小排列。即

可以发现，每个物品相当于有两个值。j的两个值都小于i时就可以转移。
把其中的某一个权值排序，然后用树状数组（或者线段树）维护另一个权值就好了（这里需要离散化）。
每次转移都是前缀最大值进行转移。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;

const int maxn = 1e5+5;
int t[maxn],p[maxn],v[maxn];
int w,n;
int uninum;
                              //树状数组是怎么解决二维的限制条件的呢?遍历顺序和数组下标(离散化)
                              //也就是第a次在b位置更新val[a]的值
class BIT{ 
    public: 
        void update(int pos,int val){
            for(; pos<=n; pos+=(-pos)&pos){
                B[pos] = max(B[pos], val);
            }
        }
        int query(int pos){     //查询是直接查前缀的结果,即1~pos
            int res=0;
            for(; pos>=1; pos-=(-pos)&pos){
                res = max(res, B[pos]);
            }
            return res;
        }
        void init(){
            memset(B,0,sizeof(B));
        }
    private:
        int B[maxn];
}BI;

struct Data{
    int t,p,v;
    int a,b;
    bool operator < (const Data &A) const{
        return a<A.a;
    }
}s[maxn];

struct Unique_Data{
    int b,id;
    bool operator < (const Unique_Data & U) const{
        return b<U.b;
    }
}uni[maxn];

void Unique(){
    sort(uni+1, uni+1+n);
    uni[0].b = -2147483647;
    for(int i=1; i<=n; i++){
        if(uni[i].b != uni[i-1].b)
            uninum++;
        s[ uni[i].id ].b = uninum;
    }
}

void solve(){
    sort(s+1, s+1+n);
    BI.init();
    for(int i=1; i<=n; i++){
        BI.update(s[i].b, BI.query(s[i].b)+s[i].v);    //树状数组处理的是前缀,所以只需要更新1次就处理了一段区间
    }
    cout<<BI.query(uninum)<<endl;
}

int main(){
    ios::sync_with_stdio(false);
      cin.tie(0);
    cin>>w>>n;
    for(int i=1; i<=n; i++){
        cin>>s[i].t>>s[i].p>>s[i].v;
        s[i].a = 2*s[i].t+s[i].p;
        uni[i].b = 2*s[i].t-s[i].p;
        uni[i].id = i;
    }
    Unique();
    solve();
}