[背包九讲1]

P1.01基础背包问题
对于N个宝石，每个宝石的价值为vi，重量花费为wi。背包的总载重量为W，则试问对于一个背包这么放宝石才能使其装的宝石总价值最大。
具体思路：考虑状态，利用i表示第i个宝石，j表示当前背包的已用空间，d[i][j]就可以表示当前状况下背包内宝石的最大价值。则要求的问题可以转化为d[N][W]的求取。
然后构建状态转移方程：

d[i][j]=max{d[i−1][j],d[i−1][j−w[i]]+v[i]}d[i][j]=max{d[i−1][j],d[i−1][j−w[i]]+v[i]}
值得注意的是这里max内只有两项是因为一个宝石只有选和不选两种情况，所以DP状态转移方程的思想就是：

当前状态 = 取最优{前一状态1，前一状态2…前一状态n}

从上可以看出状态的选取很重要，并且由于是通过将最终问题不断分为前一种状态下的最优解（即最优子结构），所以要采用自底向上的方式计算，即先计算最小问题单元，并记录，然后计算后一级问题时就可以以直接调用节约时间。所以时自底向上。也就是对解空间树从计算叶子问题开始逐步推向主问题。
仔细考虑这一过程也可以发现，在逐步上推的过程中，母问题的决策方案是不会对之前的子问题造成影响的，因此这就是无后效性的表现。（叶子问题的决策->子问题1的决策->…->子问题n的决策->母问题的决策）
伪代码为：

d[0][0...W] = 0;
for i = 1->N
for j = 0->W
if(w[i] > j)
d[i][j] =d[i-1][j]
else
d[i][j] = max{d[i-1][j],d[i-1][j-w[i]]+v[i]}

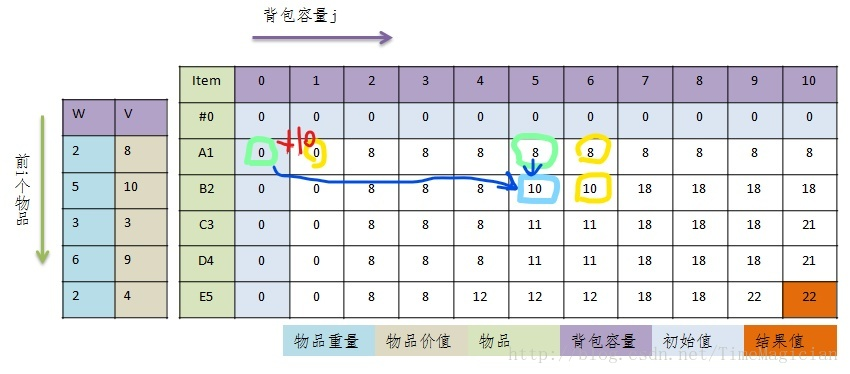
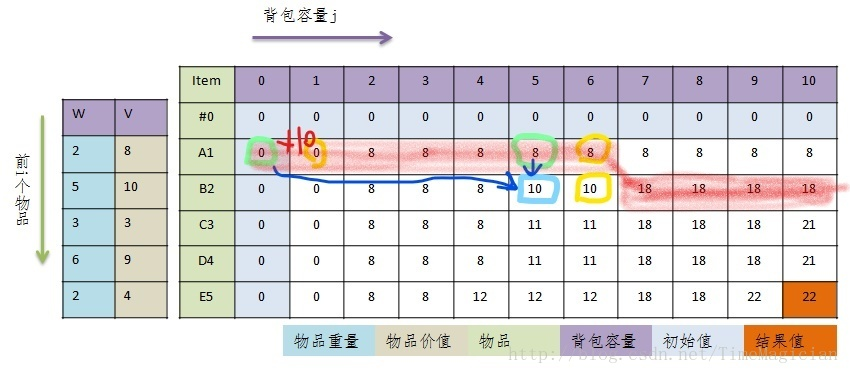
图中青色代表d[2][5]，可以看出他由绿色的两个各种中的数值得出。即当前状态由前一状态的两个解中的最优解得出。接下来黄色的三个圈也一样。因此DP的路线就是从左上角不断计算得到右下角的最终问题的解。要注意的是DP有个赋予初值的步骤。

问题优化

刚好放满的求解方法

由上图看出，如果我想求解刚好放满背包时候的背包的最大价值，可以采用的方法就是初值的赋予技巧，即只对d[0][0] = 0，d[0][1…W]都赋予负无穷，这样就可以筛选掉不满的情况。

空间的优化

从这张图里面还可以看出，每个宝石i的选择，其实只需要上一次的i-1时候的选择情况。因此其实可以用一个一维数组而不是二维数组表示。 
先看伪代码

d[0...W] = 0;
for i = 1->N
for j = W->0 //这里是唯一的不同
if(w[i] > j)
d[j] =d[j]
else
d[j] = max{d[j],d[j-w[i]]+v[i]}

伪代码只是对第二个for循环的顺序做了改变。即改为了从W到0，然后就把数组换成了一维数组。 

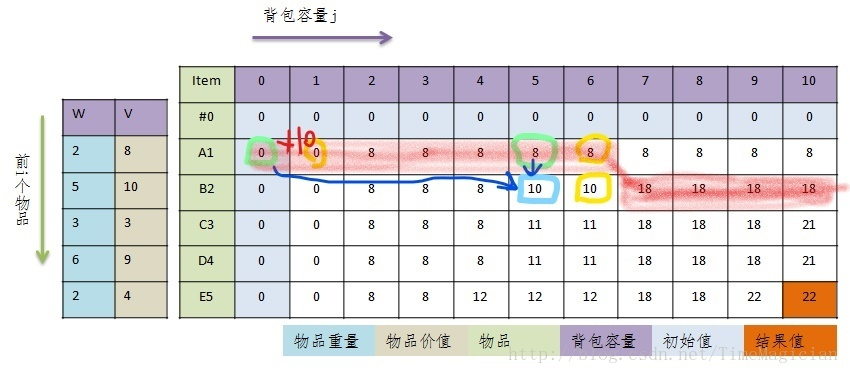
结合上图我们可以看下发生了什么。那个一维数组内存取的东西如图红色部分。是两个状态的结合。可以看出，当我要求d[2][6]时，我需要的d[1][6]和d[1][1],转换到一维数组时，就是d[6]和d[1]，然后算出来新的d[6]对原数组进行覆盖。这样就完成了空间的压缩

进一步优化

在压缩到一维数组后，其实我们还可以继续优化，即对二层循环的上下限做手脚。 
伪代码如下：

d[0...W] = 0;
for i = 1->N
for j = W->w[i] //下限不同了
/*
if(w[i] > j)
d[j] =d[j]
else
*/
d[j] = max{d[j],d[j-w[i]]+v[i]}

为何是w[i]呢？考虑下之前的情况和图，如果j

再进一步

上一节是从左边考虑遍历的节省界限。即去掉从0开始到w[i]的部分。
这一节是从右边考虑遍历的节省界限。
考虑对于结果第n个宝石，其考虑的就是d[W]项，那其前一项，其实只需要提供从W到W-w[n]项即可。如下图蓝色项。因此，对于第i个宝石时，我们指控考虑的d[j]项的范围为：W到max{w[i],W−sum(w[i],w[i+1],...,w[n])}W到max{w[i],W−sum(w[i],w[i+1],...,w[n])}

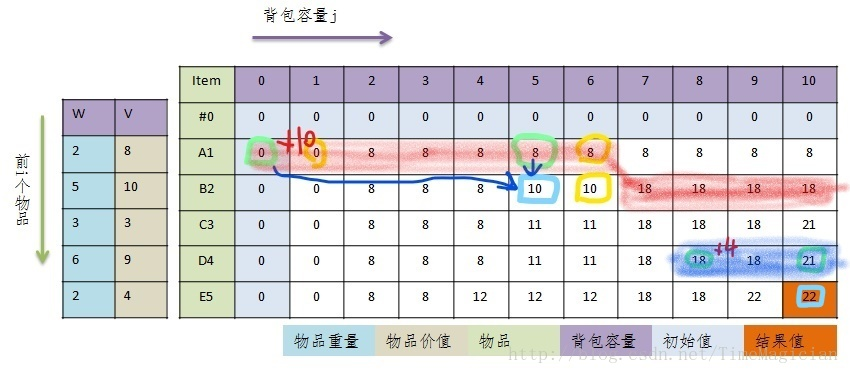
d[0...W] = 0; for i = 1->N for j = W->max{w[i],W-sum(w[i->n])} d[j] = max{d[j],d[j-w[i]]+v[i]}

public void zeroOnePack(w[i], v[i]){
for j = W->max{w[i],W-sum(w[i->n])}
d[j] = max{d[j],d[j-w[i]]+v[i]}
}

P2.完全背包问题

假若每种宝石的数量不设上限，则问题转变为完全背包问题。 
该问题的求解有两种方法，一个是基础方法，一个抽象方法。

基础方法

其实说是无限，还是有限的，即一种宝石数量肯定小于背包容量V/w[i]
考虑子状态，最直接的就是

d[i][j]=max{d[i−1][j−k∗w[i]]+k∗v[i]|0≤k≤W/w[i]}d[i][j]=max{d[i−1][j−k∗w[i]]+k∗v[i]|0≤k≤W/w[i]}
即当前状态 = 取最优{前一状态1，前一状态2…前一状态n}

改进方法是，将一种宝石ni个看成ni个统一规格的宝石，则总共有sum(n1, n2, … , nn)个宝石，大循环为
for i = 1 -> sum(n1, n2, … , nn)
这个方法只是换了个角度看问题，并没有降低代价。不过从这个角度考虑，其实我们可以考虑对同一种宝石，我们拿的个数可以等价为一颗大宝石，比如，取2颗宝石i则相当于取了一颗中2*w[i],价值2*v[i]的大宝石。
现在的情况就是如何构建各种大宝石来保证取的时候不会重复，这时候可以考虑计算机的二进制存储方式(只要有2的0，1，…，n次方的数，就可以组合出任意1到2的n次方之间的数)。构建的大宝石价值应该为1颗i，2颗i，4颗i。。。2的k次方颗i。这样，我只要对这些构造的大宝石进行是否装入判断，就可以判断出最优解是装几颗宝石i，其中k要满足w[i]∗2k≤Ww[i]∗2k≤W。
伪代码

for i = 1->N

k = 1

while(k <= W/w[i])

zeroOnePack(k*w[i],k*v[i])

k = k*2

其实上式是有冗余的，即，k不用取那么大，只要保证1，2，4，…，k的宝石加起来总的个数是小于W/w[i]的最大值就可以，而不用非要第k个是小于W/w[i]的最大值。因此构建新的k的边界应该是sum(1,2,4,…,k)<=W/w[i]时的最大值。并且为了保证总和为W/w[i]，还要再补上一颗（W/w[i]-sum(1,2,4,…,k)）*w[i]的大宝石。
伪码如下：

for i = 1->N
k = 1
amount = W/w[i]
while(k <= amount)
zeroOnePack(k*w[i],k*v[i])
amount = amount - k
k = k*2
zeroOnePack(k*w[i],k*v[i])

抽象方法—更快

还是这张图，可以看出，当初为了保证是从d[i-1][j],d[i-1][j-w[i]]推出d[i][j]，我们采用从W到w[i]的方式，其目的就是保证不会产生从d[i][0]推出[i][j]的情况，现在，既然是一个宝石i要有无限个，那么明显可以采用从d[i][0]推出[i][j]的情况，所以给出的for循环是从0->W.
伪代码如下：

d[0...W] = 0;
for i = 1->N
for j = 0->W
if(w[i] > j)
d[j] =d[j]
else
d[j] = max{d[j],d[j-w[i]]+v[i]}
我们可以定义该过程为一个新方法：

public void completePack(w[i], v[i]){
for j = 0->W
if(w[i] > j)
d[j] =d[j]
else
d[j] = max{d[j],d[j-w[i]]+v[i]}
}

P3.多重背包

多重背包在这里指的是当宝石i的个数给定为ni时的背包问题。这里可以考虑，当ni = 1时，就是01背包问题，当ni大于W/w[i]时，就是完全背包问题。当ni在两者之间时，可以转换成完全背包问题里面的基础解法。因此可以构造如下伪代码：

public void multiplePack(w[i], v[i], amount)
if(amount > W/w[i])
completePack(w[i], v[i])
else{
k = 1
amount = W/w[i]
while(k <= amount)
zeroOnePack(k*w[i],k*v[i])
amount = amount - k
k = k*2
zeroOnePack(k*w[i],k*v[i])
}

P9.背包问法变化

构造最优解

构造最优解的方法，我学到的有两种。 
第一种是采用01基础背包方案时，得到了d[i][j]，若令i = N；j = W；则可以根据求出的二维数组进行逆推求出每个最优选择。伪代码如下：

public getOptSolution(){
i = N
j = W
while(d[i][j] > d[0][j])
if d[i][j] == d[i-1][j]
没有选择第i个宝石
i = i - 1
else
选择了第i个宝石
i = i - 1
j = j - w[i]
}
第二中是采用了一维数组去进行计算的时候，特别是在求取多重背包或者完全背包问题时的构造最优解方法，关键就是建立辅助的数组进行帮忙记录，不过由于在多重背包问题时，每种宝石的具体展开大宝石数量事先计算比较麻烦，因此可以采用动态数组ArrayList来帮忙。 
伪代码：

//--------------------构造记录用动态数组（在大循环中）------------------
d[0->W] = 0
动态数组recorder
for i = 1->N
multiplePack(w[i], v[i], amount)

//--------------------改进01背包方法，增加记录数组（在小循环中）----------------

public void zeroOnePack(w[i], v[i]){
boolean[] rec
for j = W->w[i]
rec[j] = isPut(d[j],d[j-w[i]]+v[i]) //构造子方法判断，判断依据同max
d[j] = max{d[j],d[j-w[i]]+v[i]}
recorder.add(rec)

//---------------------构造最优解-------------------------
同 getOptSolution()方法

补充：
其实只要理解多重背包的基础方法，是可以不用构造记录数组也可以完成最优解的构造的。不过会比较麻烦。在此再提及一下多重背包的思想：
假设原来有N种宝石1,2,..,N.每种有n[i]个
则现在多重背包的基础方法的思想是转换成M种宝石，分别为
（n[1],2*n[1],4*n[1],…,k[1]*n[1]）,(n[2],2*n[2],4*n[2],…,k[2]*n[2]),…………….,(n[N],2*n[N],4*n[N],…,k[N]*n[N])即可。