题目描述
多米诺骨牌有上下2个方块组成,每个方块中有1~6个点。现有排成行的
上方块中点数之和记为S1,下方块中点数之和记为S2,它们的差为|S1-S2|。例如在图8-1中,S1=6+1+1+1=9,S2=1+5+3+2=11,|S1-S2|=2。每个多米诺骨牌可以旋转180°,使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。
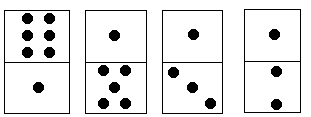
对于图中的例子,只要将最后一个多米诺骨牌旋转180°,可使上下2行点数之差为0。
输入输出格式
输入格式:
输入文件的第一行是一个正整数n(1≤n≤1000),表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数,表示多米诺骨牌上下方块中的点数a和b,且1≤a,b≤6。
输出格式:
输出文件仅一行,包含一个整数。表示求得的最小旋转次数。
输入输出样例
1
开始分析
我们先把骨牌翻转,调整至点数大的在上面
这样,我们就能保证上方的点数一定比下方大,并且保证每翻转一 次,都能使上下的点数之差变小,而变小的点数,就是上下点数之差乘以2。
把改变的点数看成物品的体积,初始上下方的点数之差看做背包体积,不难看出背包问题的模型。
那么物品的重量是什么呢?
因为我们一开始就把点数大的放在了上面,而每放一次,翻转次数就+1。考虑:要是我后来后悔了,我发现不翻这个骨牌更好怎么办?那我会把它翻回来,那么相当于没有翻这个骨牌。
因此,一开始翻过的骨牌重量就是-1,未翻过的骨牌重量就是1(重量等价于翻转次数)
当然,上下相同的骨牌就是体积为0,重量为0的物品,因为他们无论怎么翻,都不会对上下点数差造成影响。
至此,背包的模型就出来了。这个问题被简化成:有n个物品,给出每个物品的体积v[i],他们的重量是1或-1。背包的重量为sum,体积为tot,现在请把这n个物品放到背包里去,总体积不能超过tot,体积最大的情况下使得物品重量之和最小。
其中,f[i][j]表示前i件物品能装到体积为j的最小重量
s[i][j]表示前i件物品能否装到j体积
代码
#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
int v[10001],w[10001],sum,tot,ans;
int f[1001][6005],s[1001][6005];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
if(x>y)
{
v[i]=2*(x-y);
w[i]=1;
tot+=x-y;
}
if(x<y)
{
v[i]=2*(y-x);
w[i]=-1;
tot+=y-x;
sum++;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=tot;j++)
{
f[i][j]=f[i-1][j];
s[i][j]=s[i-1][j];
if(j-v[i]==0||s[i-1][j-v[i]])
{
if(!s[i][j])
{
f[i][j]=f[i-1][j-v[i]]+w[i];
s[i][j]=1;
}
else f[i][j]=min(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
for(int i=tot;i>=1;i--)
if(s[n][i])
{
printf("%d",sum+f[n][i]);
return 0;
}
return 0;
}
