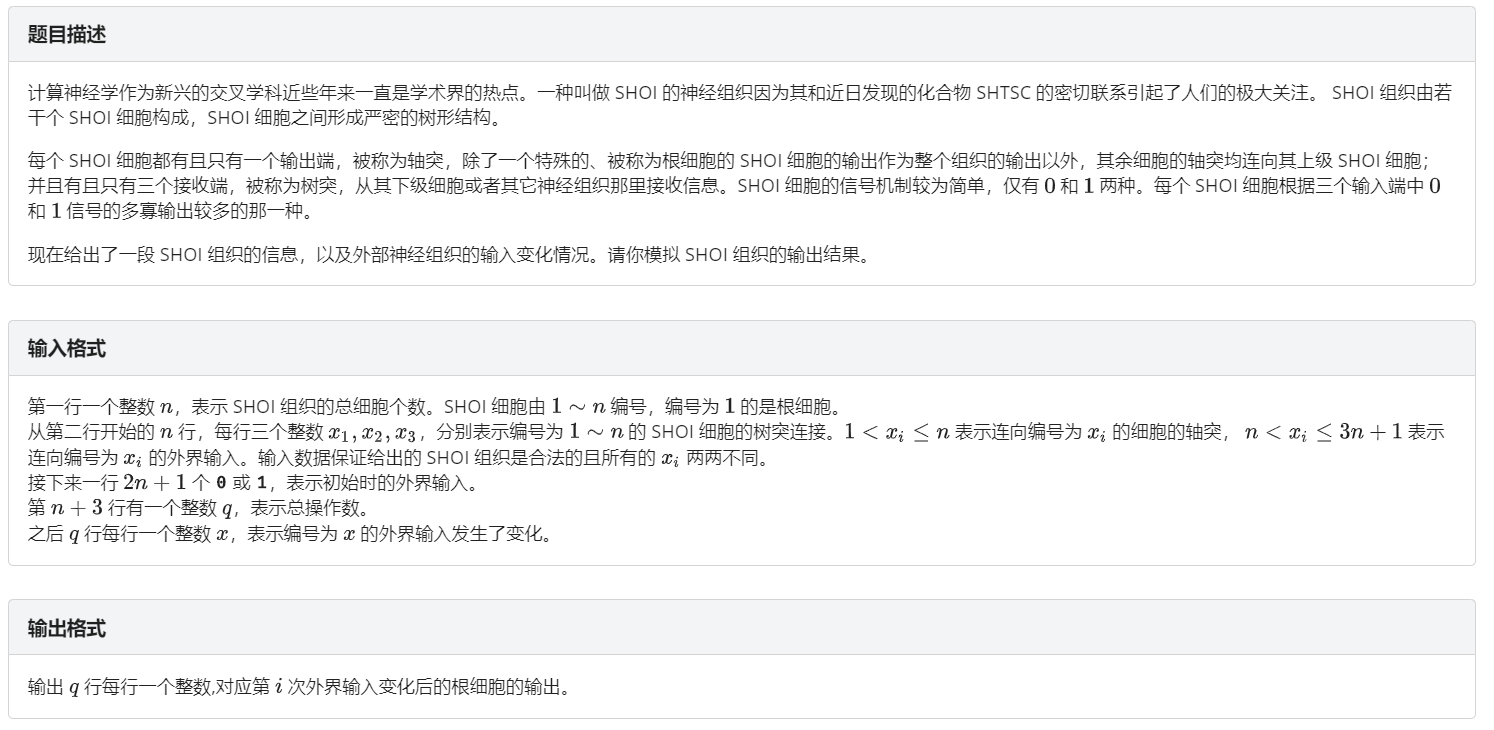
Description
Hint
(1le n, qle 5 imes 10^5)
Solution
当整棵树的某一个叶子结点发生修改时,考虑连带被改变状态的结点分布在那些位置上。
首先,一定在这个叶子结点到根结点的这条链上。其次,改变的结点一定是一段连续的链。
对于“ 改变的结点一定是一段连续的链 ” 的解释:设 ( ext{sum}(i)) 为(非叶)结点 (i) 的三个儿子中 (1) 的个数,那么从修改 ((1 ightarrow 0)) 的叶子结点的父结点开始往上,满足 ( ext{sum}(i) = 2) 的结点都要改变,直到某一个结点的 ( ext{sum}) 值 ( e 2) 了,那么这个节点就不会变(( ext{sum})值还是要改变),于是显然地这个节点的祖先也不会变(( ext{sum}) 值和点的状态都不变)。
既然如此,那我们只要找出这个“断点”,就可以转化为链上加((+1 / -1))的问题了。
两种解法:
- 轻重链剖分:时间复杂度 (O(nlog^2 n)),最后一段二分确定断点。
- ( exttt{Link-Cut Tree}):时间复杂度 (O(nlog n)),直接维护这个断点。
笔者采用了方法 2.
其实我们可以在 splay 中的结点维护两个子段:以当前结点为根的子树中深度最大的 ( ext{sum}
e 1) 或 (
e 2) 的结点编号(pos[x][0/1])。
那么 pushup 的时候,顺序是 ( ext{右子结点}
ightarrow ext{当前结点}
ightarrow ext{左子结点}):
inline void pushup(int x) {
pos[x][0] = pos[rc][0], pos[x][1] = pos[rc][1];
if (!pos[x][0]) pos[x][0] = (sum[x] != 1) ? x : pos[lc][0];
if (!pos[x][1]) pos[x][1] = (sum[x] != 2) ? x : pos[lc][1];
}
为什么这样呢?别忘了 辅助树的性质 : ( ext{splay}) 的中序遍历的结点深度递增。 这样就保证了右边的深度大于当前结点的深度,当前结点的深度大于左边的深度。其中 pos 的定义是尽可能深度大。
此外,更新加法标记也很有技巧:( ext{sum}) 值直接加,点的状态根据新的 ( ext{sum}) 重新计算,但是 ( ext{pos}) 如何更新?
答案是……直接交换!可以发现,被修改点一定是 ( ext{sum}) 值上发生了: (1 leftarrow 2) 或 (2 leftarrow 1)。于是本质上就是 swap 了一下。
inline void setAdd(int x, int v) {
sum[x] += v, val[x] = (sum[x] > 1);
swap(pos[x][0], pos[x][1]), add[x] += v;
}
其他的……基本就是基础 LCT。对了,这个题不需要换根,即不需要 reverse。
接下来是主函数。单独把这个拿出来是因为细节实在是太多了。答案 ( ext{ans}) 单独在主函数中维护。
首先,由于叶结点的特殊性,修改只能从 目标叶子结点的父结点开始 修改,然后单点修改叶子节点。
其次,如果 pos 值为 (0) 说明一路上没有阻挡的结点,直接更新到 (1) 号根节点,并且 ( ext{ans} leftarrow ext{ans} oplus 1)。
详见代码:
Code
/*
* Author : _Wallace_
* Source : https://www.cnblogs.com/-Wallace-/
* Problem : LOJ #2187 SHOI2014 三叉神经树
*/
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 5e5 + 5;
const int S = N * 3;
int ch[S][2], fa[S];
int add[S], sum[S], val[S];
int pos[S][2];
#define lc ch[x][0]
#define rc ch[x][1]
inline bool isRoot(int x) {
return x != ch[fa[x]][0] && x != ch[fa[x]][1];
}
inline int getc(int x) {
return x == ch[fa[x]][1];
}
inline void pushup(int x) {
pos[x][0] = pos[rc][0], pos[x][1] = pos[rc][1];
if (!pos[x][0]) pos[x][0] = (sum[x] != 1) ? x : pos[lc][0];
if (!pos[x][1]) pos[x][1] = (sum[x] != 2) ? x : pos[lc][1];
}
inline void setAdd(int x, int v) {
sum[x] += v, val[x] = (sum[x] > 1);
swap(pos[x][0], pos[x][1]), add[x] += v;
}
inline void pushdown(int x) {
if (!add[x]) return;
if (lc) setAdd(lc, add[x]);
if (rc) setAdd(rc, add[x]);
add[x] = 0;
}
inline void pushdownAll(int x) {
if (!isRoot(x)) pushdownAll(fa[x]);
pushdown(x);
}
inline void rotate(int x) {
int y = fa[x], z = fa[y];
int k = getc(x), w = ch[x][!k];
if (!isRoot(y)) ch[z][getc(y)] = x;
ch[x][!k] = y, ch[y][k] = w;
if (w) fa[w] = y;
fa[y] = x, fa[x] = z;
pushup(y), pushup(x), pushup(z);
}
inline void splay(int x) {
pushdownAll(x);
for (register int y = fa[x]; !isRoot(x); rotate(x), y = fa[x])
if (!isRoot(y)) rotate(getc(x) != getc(y) ? x : y);
pushup(x);
}
inline void access(int x) {
for (register int y = 0; x; x = fa[y = x])
splay(x), rc = y, pushup(x);
}
vector<int> G[S];
int n, q;
void Dfs(int x, int f) {
sum[x] = 0;
for (vector<int>::iterator it = G[x].begin(); it != G[x].end(); it++)
if (f != *it) {
Dfs(*it, x);
sum[x] += val[*it];
}
if (x <= n) val[x] = (sum[x] > 1);
}
signed main() {
ios::sync_with_stdio(false);
cin >> n;
for (register int i = 1; i <= n; i++)
for (register int j = 0, x; j < 3; j++) {
cin >> x;
G[x].push_back(i);
G[i].push_back(x);
fa[x] = i;
}
for (register int i = n + 1; i <= n * 3 + 1; i++)
cin >> val[i];
Dfs(1, 0);
int ans = val[1];
for (cin >> q; q; --q) {
int last, x, v, w;
cin >> last, x = fa[last], v = val[last] ? -1 : 1;
access(x), splay(x), w = pos[x][val[last]];
if (w) {
splay(w);
setAdd(ch[w][1], v);
pushup(ch[w][1]);
sum[w] += v;
val[w] = (sum[w] > 1);
pushup(w);
} else {
ans ^= 1;
setAdd(x, v);
pushup(x);
}
val[last] ^= 1;
cout << ans << '
';
}
}