【题解】NOI 系列题解总集

每次做一道 NOI 系列的估计都很激动吧，对于我这种萌新来说（

---

P1731 [NOI1999]生日蛋糕

练习剪枝技巧，关于剪枝，欢迎看我的垃圾无意义笔记

这道题是有一定难度的，需要运用各种高科技剪枝（？

如果泥能独立 AC 这道题，就可以拿到 NOI 铜牌了！ （不过是1999年的，现在肯定难多了

其实这道题根本不需要考虑 (pi) 因为：

[egin{aligned} V_{ ext{圆柱}} & = S_{ ext{圆柱}} imes h\ &= pi r^2 imes h\ N & = r^2 imes h end{aligned}]

[egin{aligned} S_{ ext{圆柱侧}} & = 2pi r imes h\ S &= 2rh\ S &= frac{2N}{r} end{aligned}]

因为为了方便，搜索的参数为 (5) 个：

( ext{dfs(int ceng, int nestv, int r, int h, int s);})

( ext{ceng = 当前层数， nestv = 剩余体积， r = 半径， h = 高度， s = 体积})

体积为 (100) 的栗子：画张图，更好理解：

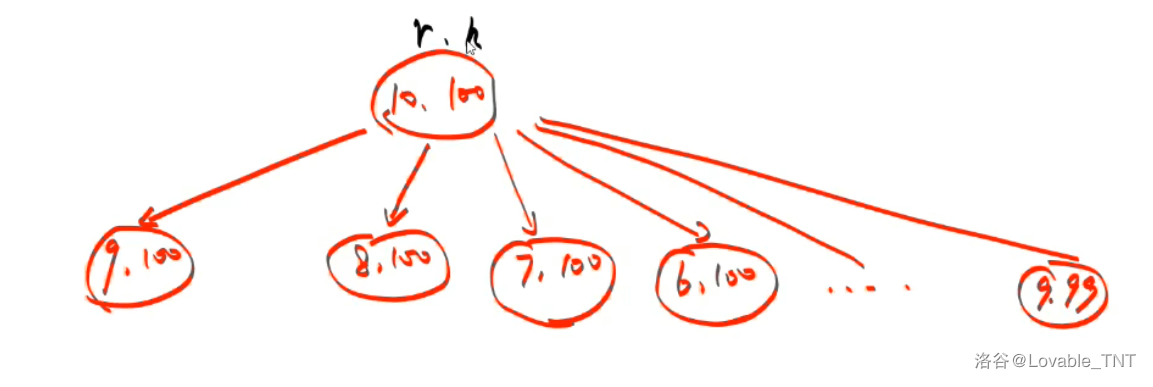
去搜每一层蛋糕的半径和高度。因为是整数，所以把所有的半径和高度枚举一遍， (r) 的根节点从 (10) 开始。从最大值到最小值，如果体积明显超出了，就可以剪枝。

枚举第一层蛋糕的高度。

此时的时间复杂度是 (O(n^2))

因为比较暴力，所以必须用到各种剪枝，在 (O(n^2)) 的基础上进行剪枝

1. 可行性剪枝

2. 最优化剪枝

3. 上下界剪枝

4. 搜索顺序剪枝

   半径从大到小，从小到大。

   高度从大到小，从小到大。

   共 4 种搜索顺序，找到最快的顺序。

最终就能 AC 本题啦~

放上 (dfs) 代码，有注释应该很好理解吧/kk：

void dfs(int ceng, int restv, int r, int h, int s) {
//ceng为已用层数，restv为剩余体积，r为当前最高层蛋糕半径，h为当前最高层蛋糕高度，s为已有表面积/π
    if(ceng == m && restv == 0) //蛋糕已完成，即层数ceng==m且体积用完 {
        ans = min(ans, s); //更新答案为最优解
        return;
    }
    if(restv < 0) return; //剩余体积小于0表示体积超过了预定的值
    if(s + 2 * restv / r >= ans) return; //若当前总表面积+该层往上所有表面积的最小和>=目前最优解
    //简单一点可以把每一层的侧面积看做最小的1，那么后续剩下部分的侧面积就等于剩余层数m-ceng
    //数据严格一点就可以从剩余体积去计算出剩余最小侧面积2 * restv / r,可改为if(s + 2 * restv / r >= ans)
    if(r * r * h * (m - ceng) < restv) return; //后续能做出蛋糕的最大体积<当前剩余体积
    for(int i = r - 1; i >= m - ceng; i--) //枚举下一层所有可能的半径
        for(int j = h - 1; j >= m - ceng; j--) //枚举下一层所有可能的高度
            if(ceng != 0) dfs(ceng + 1, restv - i * i * j, i, j, s + 2 * i * j);
            else dfs(ceng + 1, restv - i * i * j, i, j, s + 2 * i * j + i * i);
            //第一层需要计算上表面积，其他层只需计算侧面积即可，故需分类讨论
}

---