【笔记】「pj复习」深搜——简单剪枝

深搜——简单剪枝

说在最前面：

因为马上要 NOIP2020 了，所以菜鸡开始了复习qwq。

pj 组 T1 ，T2 肯定要拿到满分的，然后 T3 ， T4 拿部分分， T3 拿部分分最常见的做法就是暴搜，但是暴搜容易 T ，为了拿到更多的分数，应该合理剪枝。

各种剪枝方法

1. 优化搜索顺序

（随缘）随缘剪枝。

2. 可行性剪枝

对当前状态进行检查，发现分支无法到达递归边界，回溯。

3. 最优化剪枝 ☆☆☆ ← 最重要的一种剪枝方法

在最优化问题的搜索过程中，若当前花费的代价已超过前面搜到的最优解，回溯。

4. 上下界剪枝

按题意，找子节点的上下界。

例题

例一：洛谷 P1135 奇怪的电梯

( mLarge Link)

这道题当然 bfs 效率是最快的，但是为了练习剪枝，就可以拿 dfs 做。

思路很简单，从起点开始，只要没越界就向上下搜，全部搜完得到答案。

很容易就得到了代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#define line cout << endl
using namespace std;
const int NR = 205;
int n, a, b;
int k[NR];
int ans = 1e9;
bool flag[NR];
void dfs(int x, int step) {
	if (x < 1 || x > n || flag[x]) {
		return;
	}
	if (x == b) {
		if (step < ans) ans = step;
		return;
	}
	flag[x] = true;
	dfs(x + k[x], step + 1);
	dfs(x - k[x], step + 1);
	flag[x] = false;
}
int main() {
	cin >> n >> a >> b;
	for (int i = 1; i <= n; i++) {
		cin >> k[i];
	}
	dfs(a, 0);
	if (ans == 1e9) cout << "-1";
	else cout << ans;
	return 0;
}

很好，发现得分 (80pts) 。有两个点 T 了。

所以我们就需要剪枝。

怎么剪枝？

我们要球的是最优解，所以就可以用 最优剪枝 ，如果当前的 (step) 已经超过了最优解 (ans) ，那么就可以结束了，这样就剪枝成功，最后放上 (dfs) 代码：

void dfs(int x, int step) {
	if (x < 1 || x > n || flag[x] || step >= ans) {
		return;
	}
	if (x == b) {
		if (step < ans) ans = step;
		return;
	}
	flag[x] = true;
	dfs(x + k[x], step + 1);
	dfs(x - k[x], step + 1);
	flag[x] = false;
}

当然了，这题如果拿 (bfs) 做肯定是不会 T 的，但是为了练习剪枝嘛~ qwq

例二：洛谷 P1731 [NOI1999]生日蛋糕

( mLarge Link)

这道题是有一定难度的，需要运用各种高科技剪枝（？

如果泥能独立 AC 这道题，就可以拿到 NOI 铜牌了！ （不过是1999年的，现在肯定难多了

其实这道题根本不需要考虑 (pi) 因为：

[egin{aligned} V_{ ext{圆柱}} & = S_{ ext{圆柱}} imes h\ &= pi r^2 imes h\ N & = r^2 imes h end{aligned}]

[egin{aligned} S_{ ext{圆柱侧}} & = 2pi r imes h\ S &= 2rh\ S &= frac{2N}{r} end{aligned}]

因为为了方便，搜索的参数为 (5) 个：

( ext{dfs(int ceng, int nestv, int r, int h, int s);})

( ext{ceng = 当前层数， nestv = 剩余体积， r = 半径， h = 高度， s = 体积})

体积为 (100) 的栗子：画张图，更好理解：

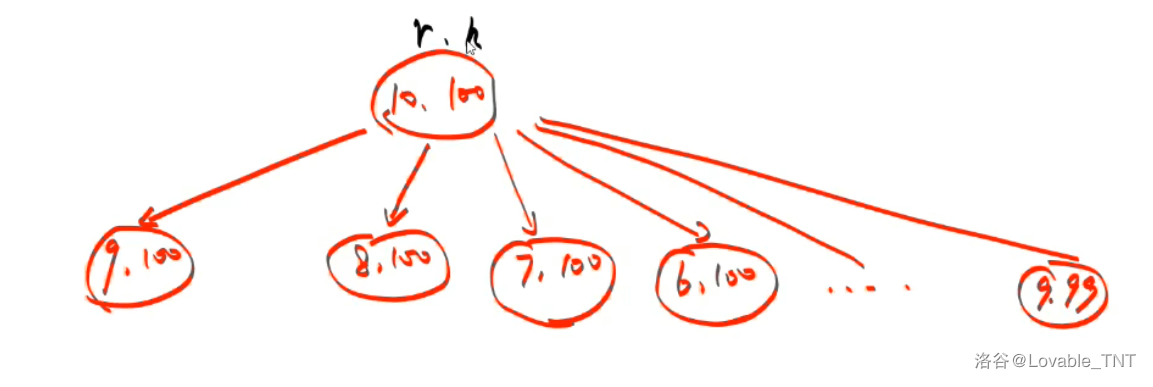
去搜每一层蛋糕的半径和高度。因为是整数，所以把所有的半径和高度枚举一遍， (r) 的根节点从 (10) 开始。从最大值到最小值，如果体积明显超出了，就可以剪枝。

枚举第一层蛋糕的高度。

此时的时间复杂度是 (O(n^2))

因为比较暴力，所以必须用到各种剪枝，在 (O(n^2)) 的基础上进行剪枝

1. 可行性剪枝

2. 最优化剪枝

3. 上下界剪枝

4. 搜索顺序剪枝

   半径从大到小，从小到大。

   高度从大到小，从小到大。

   共 4 种搜索顺序，找到最快的顺序。

最终就能 AC 本题啦~

放上 (dfs) 代码，有注释应该很好理解吧/kk：

void dfs(int ceng, int restv, int r, int h, int s) {
//ceng为已用层数，restv为剩余体积，r为当前最高层蛋糕半径，h为当前最高层蛋糕高度，s为已有表面积/π
    if(ceng == m && restv == 0) //蛋糕已完成，即层数ceng==m且体积用完 {
        ans = min(ans, s); //更新答案为最优解
        return;
    }
    if(restv < 0) return; //剩余体积小于0表示体积超过了预定的值
    if(s + 2 * restv / r >= ans) return; //若当前总表面积+该层往上所有表面积的最小和>=目前最优解
    //简单一点可以把每一层的侧面积看做最小的1，那么后续剩下部分的侧面积就等于剩余层数m-ceng
    //数据严格一点就可以从剩余体积去计算出剩余最小侧面积2 * restv / r,可改为if(s + 2 * restv / r >= ans)
    if(r * r * h * (m - ceng) < restv) return; //后续能做出蛋糕的最大体积<当前剩余体积
    for(int i = r - 1; i >= m - ceng; i--) //枚举下一层所有可能的半径
        for(int j = h - 1; j >= m - ceng; j--) //枚举下一层所有可能的高度
            if(ceng != 0) dfs(ceng + 1, restv - i * i * j, i, j, s + 2 * i * j);
            else dfs(ceng + 1, restv - i * i * j, i, j, s + 2 * i * j + i * i);
            //第一层需要计算上表面积，其他层只需计算侧面积即可，故需分类讨论
}

好啦！窝拿到 NOI 铜牌啦啊！（雾