三分模版

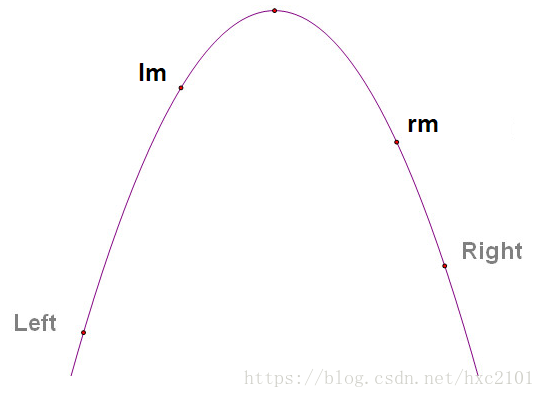
三分查找，用来比较不同坐标处值的大小关系（比较的这两点通常是分布在极值点两侧的），来确定区间内的极值。

三分应用于最优化问题的求解。在解题时没必要给出证明，只要知道问题不满足单调性，就可以尝试用三分搜索极值点，而且三分整数很少见，因为除非能够证明这种策略是正确的(即完全符合凸函数的性质，但是通常极值点不会在整点取得，如果三分整数，那么函数也不是连续的了)，否则很可能会错误，而三分应用在小数中是最常见的，比如说三分角度，三分坐标等等。

一些函数的常用结论：

1、如果一个函数是若干个开口向上的二次函数的最大值 这个函数只能先减后增

2、如果一个函数是若干个开口向下的二次函数的最小值 这个函数只能先增后减

模版：

凸函数求极大值：

while (l + eps < r) {
        double lm = l + (r-l) / 3;
        double rm = r - (r-l) / 3;
        if (f(lm) > f(rm))
            r = rm;
        else
            l = lm;
    }
    //凸点：    l
    cout << f(l) << endl;

凹函数求极小值：

while (l + eps < r) {
        double m1 = l + (r-l) / 3;
        double m2 = r - (r-l) / 3;
        if (f(m1) > f(m2))
            l = m1;
        else
            r = m2;
    }
    // 凹点：   l
    cout << f(l) << endl;