题目链接:http://oj.ecustacm.cn/problem.php?id=1286
题目描述
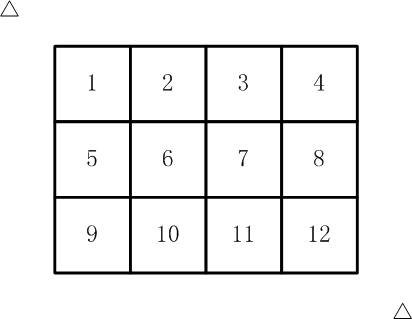
如下图, 有12张连在一起的12生肖的邮票。现在你要从中剪下5张来,要求必须是连着的。(仅仅连接一个角不算相连)
比如,下面两张图中,粉红色所示部分就是合格的剪取。
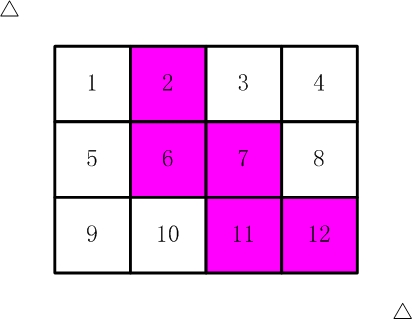
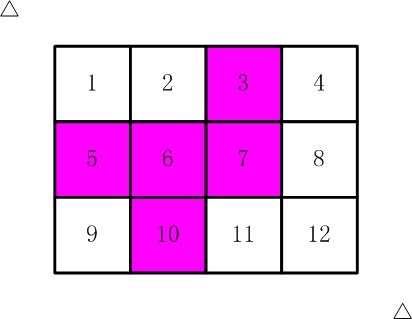
请你计算,一共有多少种不同的剪取方法。

比如,下面两张图中,粉红色所示部分就是合格的剪取。


请你计算,一共有多少种不同的剪取方法。
输出
请填写表示方案数目的整数。
思想:
一看数据量应该就知道是一个简单的 DFS 或者 BFS 的题目,但是这道题的难点在于如何避免重复的
这里采取的想法其实就是把每个方格看成二进制的一个位,然后看所有位算出的十进制的数字是否一样
#include <iostream> #include <algorithm> #include <string> #include <string.h> #include <vector> #include <map> #include <stack> #include <set> #include <queue> #include <math.h> #include <cstdio> #include <iomanip> #include <time.h> #include <list> #define LL long long #define INF 0x3f3f3f3f #define ls nod<<1 #define rs (nod<<1)+1 const int maxn = 1e5 + 10 ; const LL mod = 20010905; int vis[10][10],hash[maxn]; int ans; int dir[4][2] = {{-1,0},{1,0},{0,1},{0,-1}}; void dfs(int cnt) { if (cnt == 5) { int temp = 0; for (int i = 1;i <= 3;i++) { for (int j = 1;j <= 4;j++) { temp += vis[i][j]; temp = temp << 1; } } if (!hash[temp]) { ans++; hash[temp] = 1; } return ; } for (int i = 1;i <= 3;i++) { for (int j = 1;j <= 4;j++) { if (vis[i][j]) { for (int k = 0; k < 4; k++) { int x = i + dir[k][0]; int y = j + dir[k][1]; if (x <= 0 || x > 3 || y <= 0 || y > 4) continue; if (!vis[x][y]) { vis[x][y] = 1; dfs(cnt + 1); vis[x][y] = 0; } } } } } } int main() { ans = 0; for (int i = 1;i <= 3;i++) { for (int j = 1;j <= 4;j++) { vis[i][j] = 1; dfs(1); vis[i][j] = 0; } } printf("%d ",ans); return 0; }