Codeforces Round #595 (Div. 3)

有一个长度为n的序列a1，a2...an，将他们分为若干组，使得每一组没有两个数的差为1，使分的组数尽可能少。

思路：
将数组排序之后从前往后遍历，如果出现了两个数的差值为1 那么就得分两组否则一组

 1 #include <math.h>
 2 #include <stdio.h>
 3 #include <stdlib.h>
 4 #include <iostream>
 5 #include <algorithm>
 6 #include <string>
 7 #include <string.h>
 8 #include <vector>
 9 #include <map>
10 #include <stack>
11 #include <set>
12 //#include <random>
13  
14 #define LL long long
15 #define INF 0x3f3f3f3f
16 #define ls nod<<1
17 #define rs (nod<<1)+1
18 const int maxn = 2e5 + 10;
19 const double eps = 1e-9;
20  
21 int arr[maxn];
22 int main() {
23     int T;
24     scanf("%d",&T);
25     while (T--) {
26         int n;
27         scanf("%d",&n);
28         for (int i=1;i<=n;i++) {
29             scanf("%d",&arr[i]);
30         }
31         std::sort(arr+1,arr+1+n);
32         if (n == 1) {
33             printf("1
");
34             continue;
35         }
36         bool flag = false;
37         for (int i=2;i<=n;i++) {
38             if (arr[i] - arr[i-1] <= 1) {
39                 flag = true;
40             }
41         }
42         if (flag) {
43             printf("2
");
44         }
45         else
46             printf("1
");
47     }
48     return 0;
49 }

B1、B2 - Books Exchange (easy version)

有n个孩子，每个孩子都在读一本独特的书。在任何一天结束时，第i个孩子将把他的书交给第pi个孩子（如果i = pi，则该孩子将把他的书交给他自己）。保证pi的所有值都是从1到n的不同整数（即p是一个排列）。序列p每天都不变化，它是固定的。

例如，如果n = 6且p = [4,6,1,3,5,2]，则在第一天结束时，第一个孩子的书将属于第四个孩子，第二个孩子-第二个孩子将属于第六个孩子，依此类推。在第二天结束时，第一个孩子的书将属于第三个孩子，第二个孩子将属于第二个孩子，依此类推。

您的任务是确定从1到n的每个i，第i个孩子的书第一次返还给他的天数。

考虑以下示例：p = [5,1,2,4,3]。第一个孩子的书将传递给以下孩子：

第一天之后，它将属于第五个孩子，第2天之后，它将属于第3个孩子，第三天之后，它将属于第二个孩子，在第4天之后，它将属于第一个孩子。因此，第四天之后，第一个孩子的书将归还其所有者。第四天的书将在整整一天后第一次归还给他。

您必须回答q个独立查询。

输入

输入的第一行包含一个整数q（1≤q≤200）-查询数。然后q查询。

查询的第一行包含一个整数n（1≤n≤200）-查询中孩子的数量。查询的第二行包含n个整数p1，p2，…，pn（1≤pi≤n，所有pi都是唯一的，即p是排列），其中pi是将得到第i个书的孩子小子

输出

对于每个查询，在其上打印答案：n个整数a1，a2，…，an，其中ai是该查询中第i个孩子的书第一次还给他的天数。

以样例为例

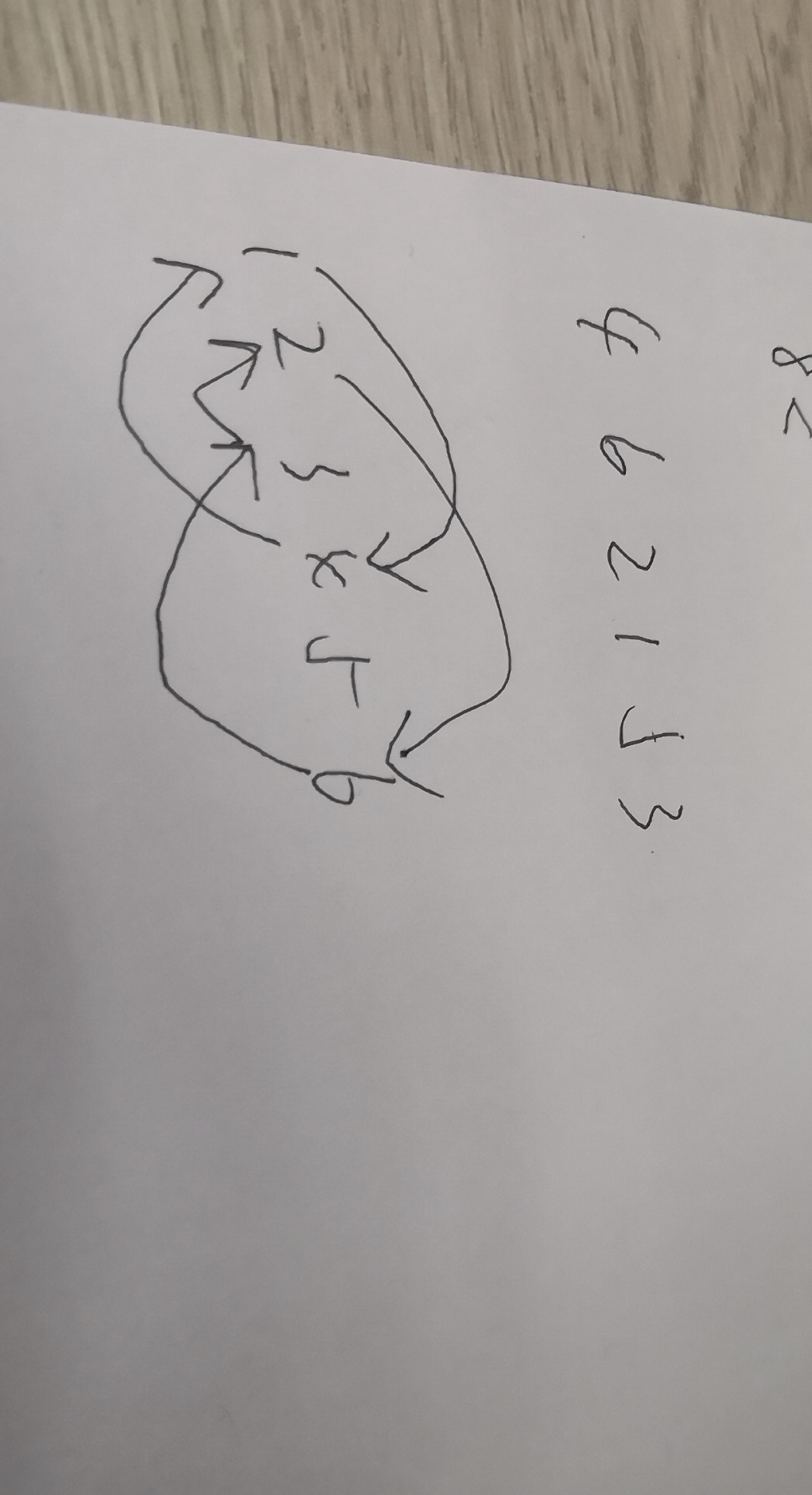
会发现环上的每个开始到第一次回到自己手中的天数都是一样的

 1 #include <math.h>
 2 #include <stdio.h>
 3 #include <stdlib.h>
 4 #include <iostream>
 5 #include <algorithm>
 6 #include <string>
 7 #include <string.h>
 8 #include <vector>
 9 #include <map>
10 #include <stack>
11 #include <set>
12 //#include <random>
13  
14 #define LL long long
15 #define INF 0x3f3f3f3f
16 #define ls nod<<1
17 #define rs (nod<<1)+1
18 const int maxn = 2e5 + 10;
19 const double eps = 1e-9;
20  
21 int fa[maxn],arr[maxn];
22 int cnt;
23 void dfs(int i,int j) {
24     cnt++;
25     if (arr[i] == j) {
26         fa[i] = cnt;
27         return ;
28     }
29     else {
30         dfs(arr[i],j);
31         fa[i] = cnt;
32     }
33 }
34 int main() {
35     int T;
36     scanf("%d",&T);
37     while (T--) {
38         int n;
39         scanf("%d",&n);
40         for (int i=1;i<=n;i++) {
41             scanf("%d",&arr[i]);
42             fa[i] = 0;
43         }
44         for (int i=1;i<=n;i++) {
45             if (fa[i] == 0) {
46                 cnt = 0;
47                 dfs(i,i);
48             }
49         }
50         for (int i=1;i<=n;i++) {
51             printf("%d ",fa[i]);
52         }
53         printf("
");
54     }
55     return 0;
56 }

C1、C2 Good Numbers (hard version)

现在给出一个定义：Good Number（下文以好数代替），好数是指可以变成

例如：

$30=3^3+3^130=33+31$

$1=3^01=30$

$12=3^2+3^112=32+31$

$不是好数，因为2=3^0+3^02=30+30，不符合不同次幂的条件$

$不是好数，例如19=3^2+3^2+3^0=3^2+3^1+3^1+3^1+3^019=32+32+30=32+31+31+31+30，不符合不同次幂的条件$

现在给你一些正整数

输入格式

输入第一行为一个正整数

然后有 $qq行，每行一个正整数n(1≤n≤10^4)n(1≤n≤104)$

输出格式

对于每个nnn，输出最小的

$思路：$

$转化成三进制来看。其实就是判断有没有出现2 ，如果没有那就输出它自己如果出现了就往前找$

感谢机房大佬魏队的思路

  1 #include <math.h>
  2 #include <stdio.h>
  3 #include <stdlib.h>
  4 #include <iostream>
  5 #include <algorithm>
  6 #include <string>
  7 #include <string.h>
  8 #include <vector>
  9 #include <map>
 10 #include <stack>
 11 #include <set>
 12 //#include <random>
 13  
 14 #define LL long long
 15 #define INF 0x3f3f3f3f
 16 #define ls nod<<1
 17 #define rs (nod<<1)+1
 18 const int maxn = 2e5 + 10;
 19 const double eps = 1e-9;
 20  
 21 LL arr[40] = {1,3,9,27,81,243,729,2187,6561,19683,59049,177147,531441,1594323,4782969,14348907,43046721,129140163,387420489,1162261467,3486784401,10460353203,31381059609,94143178827,282429536481,847288609443,2541865828329,7625597484987,22876792454961,68630377364883,205891132094649,617673396283947,1853020188851841,5559060566555523,16677181699666569,50031545098999707,150094635296999121,450283905890997363,1350851717672992089,4052555153018976267};
 22 int vis[20] = {0};
 23 LL bit[110];
 24  
 25  
 26 LL mul(LL a,LL b)
 27 {
 28     LL sum = 1;
 29     while (b>0)
 30     {
 31         if (b%2==1) // b是奇数
 32         {
 33             sum = (a*sum);
 34         }
 35         a = (a*a) ;
 36         b = b/2;
 37     }
 38     return sum;
 39 }
 40  
 41 LL binarySearch(LL a[],LL n,LL key)
 42 {
 43     LL left = 0;
 44     LL right = n-1;
 45     while (left <= right )
 46     {
 47         LL mid = (left + right) / 2;
 48         if (a[mid] > key)
 49             right = mid - 1;
 50         else if (a[mid] <= key)
 51             left = mid + 1;
 52     }
 53     if (a[right] <= key && !vis[right])
 54         return right;
 55     if (a[right] <= key) {
 56         while (vis[right]) {
 57             right--;
 58         }
 59         return right;
 60     }
 61     return right;
 62 }
 63  
 64 int check(LL k) {
 65     memset(vis,0, sizeof(vis));
 66     while (k) {
 67         LL idex = binarySearch(arr, 40, k);
 68         if (idex >= 0) {
 69             vis[idex] = 1;
 70             k -= arr[idex];
 71         }
 72         else {
 73             return 0;
 74         }
 75     }
 76     return 1;
 77 }
 78  
 79  
 80 int main() {
 81     int T;
 82     scanf("%d",&T);
 83     while (T--) {
 84         LL n;
 85         scanf("%lld",&n);
 86         LL nn = n;
 87         LL sum = 0;
 88         int tot = 0;
 89         while (n) {
 90             bit[++tot] = n % 3;
 91             n /= 3;
 92         }
 93         LL i;
 94         for (i=tot;i>=1;i--) {
 95             if (bit[i] == 2) {
 96                 break;
 97             }
 98         }
 99         if (!i) {
100             printf("%lld
",nn);
101         }
102         else {
103             i++;
104             for (;;i++) {
105                 if (bit[i] == 0 || i > tot) {
106                     bit[i] = 1;
107                     break;
108                 }
109             }
110             if (i > tot)
111                 sum += mul(3,i-1);
112             for (;i<=tot;i++) {
113                 if (bit[i] == 1) {
114                     sum += mul(3,i-1);
115                 }
116             }
117             printf("%lld
",sum);
118         }
119     }
120     return 0;
121 }

D1、D2 Too Many Segments

给予 $nn条线段，这些线段可以有重叠部分甚至完全重叠在一起。第ii条线段[l_i,r_i](l_i≤r_i)[li,ri](li≤ri)覆盖了所有整数点jj满足l_i≤j≤r_ili≤j≤ri$

如果一个整数点被超过

你的任务是去掉最少的线段使得没有坏点的存在

输入格式

输入第一行是两个正整数， $nn和kk(1≤k≤n≤2*10^5)(1≤k≤n≤2∗105)$

然后有 $nn行，每行两个正整数，其中的第ii行表示第ii条线段的两个端点l_ili和r_iri(1≤l_i≤r_i≤2*10^5)(1≤li≤ri≤2∗105)$

输出格式

输出的第一行为一个整数

第二行输出 $mm个不同的正整数p_1,p_2,…p_m(1≤p_i≤n)p1,p2,…pm(1≤pi≤n)表示你移除了的线段的编号。如果有不止一个答案，可以输出任意一个满足条件的答案。$

$思路：$

$将右端点进行排序，然后我们从左端点开始取。并采取 set 进行维护，如果超过了 k ，那么直接删去最后一个就可以了，因为它是最长的！$

这题同样感谢机房大佬魏队给思路

 1 #include <math.h>
 2 #include <stdio.h>
 3 #include <stdlib.h>
 4 #include <iostream>
 5 #include <algorithm>
 6 #include <string>
 7 #include <string.h>
 8 #include <vector>
 9 #include <map>
10 #include <stack>
11 #include <set>
12 //#include <random>
13  
14 #define LL long long
15 #define INF 0x3f3f3f3f
16 #define ls nod<<1
17 #define rs (nod<<1)+1
18 const int maxn = 2e5 + 10;
19 const double eps = 1e-9;
20  
21 struct Node {
22     int y;
23     int idex;
24 };
25  
26 bool operator<(Node a,Node b) {
27     if (a.y != b.y)
28         return a.y < b.y;
29     else
30         return a.idex < b.idex;
31 }
32  
33 std::vector<Node> g[maxn];
34 std::vector<int> out;
35  
36 int main() {
37     int n,k;
38     scanf("%d%d",&n,&k);
39     for (int i=1;i<=n;i++) {
40         int x,y;
41         scanf("%d%d",&x,&y);
42         Node a;
43         a.y = y;
44         a.idex = i;
45         g[x].push_back(a);
46     }
47     std::set<Node> st;
48     for (int i=1;i<maxn;i++) {
49         while (st.size() && (*st.begin()).y < i)
50             st.erase(*st.begin());
51         for (int j=0;j<g[i].size();j++) {
52             st.insert(g[i][j]);
53         }
54         while (st.size() > k) {
55             out.push_back((*st.rbegin()).idex);
56             st.erase(*st.rbegin());
57         }
58     }
59     int len = out.size();
60     printf("%d
",len);
61     for (int i=0;i<len;i++) {
62         printf("%d ",out[i]);
63     }
64     printf("
");
65     return 0;
66 }

E - By Elevator or Stairs?

思路：

傻逼DP

dp[i][0] 代表坐电梯，dp[i][1] 代表走楼梯

转移方程：

dp[i][0] = min(dp[i][0] + b[i-1],dp[i][1] + c + b[i-1])

dp[i][1] = min(dp[i-1][0],dp[i-1][1]) + a[i-1]

 1 #include <math.h>
 2 #include <stdio.h>
 3 #include <stdlib.h>
 4 #include <iostream>
 5 #include <algorithm>
 6 #include <string>
 7 #include <string.h>
 8 #include <vector>
 9 #include <map>
10 #include <stack>
11 #include <set>
12 //#include <random>
13 
14 #define LL long long
15 #define INF 0x3f3f3f3f
16 #define ls nod<<1
17 #define rs (nod<<1)+1
18 const int maxn = 2e5 + 10;
19 const double eps = 1e-9;
20 
21 int n,c;
22 int a[maxn],b[maxn],dp[maxn][2];
23 
24 int main() {
25     scanf("%d%d",&n,&c);
26     for (int i=1;i<n;i++) {
27         scanf("%d",&a[i]);
28     }
29     for (int i=1;i<n;i++) {
30         scanf("%d",&b[i]);
31     }
32     dp[1][0] = c;
33     dp[1][1] = 0;
34     for (int i=2;i<=n;i++) {
35         dp[i][0] = std::min(dp[i-1][0] + b[i-1], dp[i-1][1] + c + b[i-1]);
36         dp[i][1] = std::min(dp[i-1][0], dp[i-1][1]) + a[i-1];
37     }
38     for (int i=1;i<n;i++) {
39         printf("%d ",std::min(dp[i][0],dp[i][1]));
40     }
41     printf("%d
",std::min(dp[n][0],dp[n][1]));
42     return 0;
43 }

相关阅读:
实现分布式爬虫
 hadoop安装文档
 远程连接mysql和redis配置
 scrapy(2)
10月10号动手动脑
 10月6日和动手动脑
 10月4日
 课程总结
 又学java的第一天
 第一节测试总结
原文地址：https://www.cnblogs.com/-Ackerman/p/11761508.html