划分树,类似线段树,主要用于求解某个区间的第k 大元素(时间复杂度log(n)),快排本也可以快速找出,但快排会改变原序列,所以每求一次都得恢复序列。
什么是划分树?
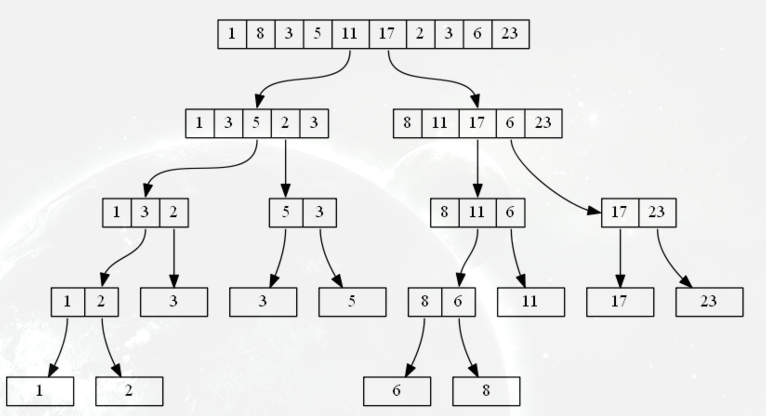
划分树是一种基于线段树的数据结构,也利用了分治的思想,却比线段树高效很多,这是为什么?因为划分树又多了一个性质:在划分时不是随意划分,也不是排序后直接划分(因为这样会破坏原有结构),而是排序后仍保持原来的相对顺序再分到左右子树。
具体实现方法:
整个过程分为建树和查询两个阶段:
1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 #include<algorithm> 5 using namespace std; 6 7 const int MAXN=100010; 8 int tree[30][MAXN];//表示每层每个位置的值 9 int sorted[MAXN];//已经排序的数 10 int toleft[30][MAXN];//toleft[p][i]表示第i层从1到i有多少个数分入左边 11 12 void build(int l,int r,int dep) 13 { 14 if(l==r)return; 15 int mid=(l+r)>>1; 16 int same=mid-l+1;//表示等于中间值而且被分入左边的个数 17 for(int i=l;i<=r;i++) 18 if(tree[dep][i]<sorted[mid]) 19 same--; 20 int lpos=l; 21 int rpos=mid+1; 22 for(int i=l;i<=r;i++) 23 { 24 if(tree[dep][i]<sorted[mid])//比中间的数小,分入左边 25 tree[dep+1][lpos++]=tree[dep][i]; 26 else if(tree[dep][i]==sorted[mid]&&same>0) 27 { 28 tree[dep+1][lpos++]=tree[dep][i]; 29 same--; 30 } 31 else //比中间值大分入右边 32 tree[dep+1][rpos++]=tree[dep][i]; 33 toleft[dep][i]=toleft[dep][l-1]+lpos-l;//从1到i放左边的个数 34 35 } 36 build(l,mid,dep+1); 37 build(mid+1,r,dep+1); 38 39 } 40 41 42 //查询区间第k大的数,[L,R]是大区间,[l,r]是要查询的小区间 43 int query(int L,int R,int l,int r,int dep,int k) 44 { 45 if(l==r)return tree[dep][l]; 46 int mid=(L+R)>>1; 47 int cnt=toleft[dep][r]-toleft[dep][l-1];//[l,r]中位于左子树的个数 48 if(cnt>=k) 49 { 50 //L+要查询的区间前被放在左边的个数 51 int newl=L+toleft[dep][l-1]-toleft[dep][L-1]; 52 //左端点加上查询区间会被放在左边的个数 53 int newr=newl+cnt-1; 54 return query(L,mid,newl,newr,dep+1,k); 55 } 56 else 57 { 58 int newr=r+toleft[dep][R]-toleft[dep][r]; // 我们一开始默认左子树是满的,那么右子树的最后一个元素下标就是r,如果[r+1,R]还有属于左子树我们就加进去就好了 59 int newl=newr-(r-l-cnt); // newr = newl + (r-l+1-cnt) - 1 , (r-l+1-cnt) 代表[l,r]之间属于右子树的个数 60 return query(mid+1,R,newl,newr,dep+1,k-cnt); // 因为是查右子树了,所以 k = k - cnt 61 } 62 } 63 64 65 int main() 66 { 67 //freopen("in.txt","r",stdin); 68 //freopen("out.txt","w",stdout); 69 int T; 70 int n,m; 71 int s,t,k; 72 scanf("%d",&T); 73 while(T--) 74 { 75 scanf("%d%d",&n,&m); 76 memset(tree,0,sizeof(tree));//这个必须 77 for(int i=1;i<=n;i++)//从1开始 78 { 79 scanf("%d",&tree[0][i]); 80 sorted[i]=tree[0][i]; 81 } 82 sort(sorted+1,sorted+n+1); 83 build(1,n,0); 84 while(m--) 85 { 86 scanf("%d%d%d",&s,&t,&k); 87 printf("%d ",query(1,n,s,t,0,k)); 88 } 89 } 90 return 0; 91 }