中国剩余定理 (CRT)

中国剩余定理，又名孙子定理

能求解什么问题呢？

问题：

一堆物品

3个3个分剩2个

5个5个分剩3个

7个7个分剩2个

问这个物品有多少个

中国剩余定理给出了以下的一元线性同余方程组：

 

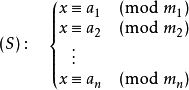
中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，

 方程组(S)

有解，并且通解可以用如下方式构造得到：

设

 

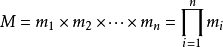是整数m1,m2, ... ,mn的乘积，并设

 

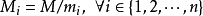是除了mi以外的n- 1个整数的乘积。

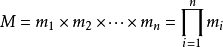
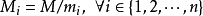
设

 

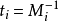这个就是逆元了

  

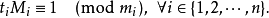
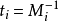
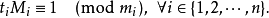
通解形式为

  

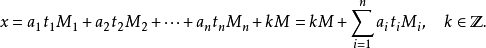在模M的意义下，方程组(S)只有一个解：

 

 

 

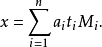
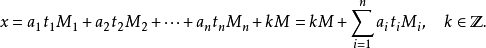
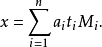
注意这样求解的一定要满足： m1,m2,....,mn 两两互质

LL inv(LL t,LL p){   // t 关于 p 的逆元
    LL x,y,d;
    d = ex_gcd(t,p,x,y);
    if (d == 1){
        return (x%p+p)%p;
    }else
        return -1;
}


// n个方程： x = a[i](mod m[i])   (0<=i<n)

LL china(int n,LL *a,LL *m){
    LL M = 1,ret = 0;
    for (int i=0;i<n;i++){
        M *= m[i];
    }
    for (int i=0;i<n;i++){
        LL w = M/m[i];
        ret = (ret + inv(w,m[i]) * w * a[i]) % M;
    }
    return (ret + M) % M;
}

但是如果遇到不是互质的模线性方程组我们要怎么办呢？

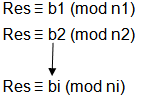
问题描述：给出bi，ni的值，且n1, n2, n3,…, ni两两之间不一定互质，求Res的值？ 
解：采用的是合并方程的做法。 
这里将以合并第一第二个方程为例进行说明 
由上图前2个方程得(设k1、k2为某一整数)： 
 
 

例题： hdu 1573 X问题 【下面已给出代码】 
http://acm.hdu.edu.cn/showproblem.php?pid=1573 

#include <iostream>
#include <algorithm>

typedef long long LL;

using namespace std;

int N;


LL ex_gcd(LL a,LL b,LL &x,LL &y){
    if (b == 0){
        x = 1;
        y = 0;
        return a;
    }
    LL gcd = ex_gcd(b,a%b,y,x);
    y -= (a/b)*x;
    return gcd;
}

LL inv(LL t,LL p){   // t 关于 p 的逆元
    LL x,y,d;
    d = ex_gcd(t,p,x,y);
    if (d == 1){
        return (x%p+p)%p;
    }else
        return -1;
}


// n个方程： x = a[i](mod m[i])   (0<=i<n)

LL china(int n,LL *a,LL *m){
    LL M = 1,ret = 0;
    for (int i=0;i<n;i++){
        M *= m[i];
    }
    for (int i=0;i<n;i++){
        LL w = M/m[i];
        ret = (ret + inv(w,m[i]) * w * a[i]) % M;
    }
    return (ret + M) % M;
}

LL CRT(LL b[],LL n[],int num){
    bool flag = false;
    LL n1 = n[0],n2,b1 = b[0],b2,bb,d,t,k,x,y;
    for (int i=1;i<num;i++){
        n2 = n[i],b2 = b[i];
        bb = b2 - b1;
        d = ex_gcd(n1,n2,x,y);
        if (bb%d){
            flag = true;
            break;
        }
        k = bb / d * x;
        t = n2 / d;
        if (t<0)
            t = -t;
        k = (k % t + t) % t;
        b1 = b1 + n1 * k;
        n1 = n1 / d * n2;
    }
    if (flag)     //无解
        return 0;
    if (b1 == 0)   // 如果解为0，题目要求正整数解，显然不可以
        b1 = n1;   // n1为所以n[i] 的最小公倍数
    if (b1>N)
        return 0;
    return (N-b1) / n1 + 1;      //形成的解：b1, b1+n1, b1+2n1,..., b1+xni...
}


int main(){
    int t,num;
    LL b[10],n[10];
    scanf("%d",&t);
    while (t--){
        scanf("%d%d",&N,&num);
        for (int i=0;i<num;i++){
            scanf("%lld",&n[i]);
        }
        for (int i=0;i<num;i++){
            scanf("%lld",&b[i]);
        }
        printf("%lld
",CRT(b,n,num));
    }
    return 0;
}