单调队列
性质
单调队列和单调栈很像,就是一个维护了单调性的队列数据结构,可以是单调递增的,也可以是单调递减的。
模型
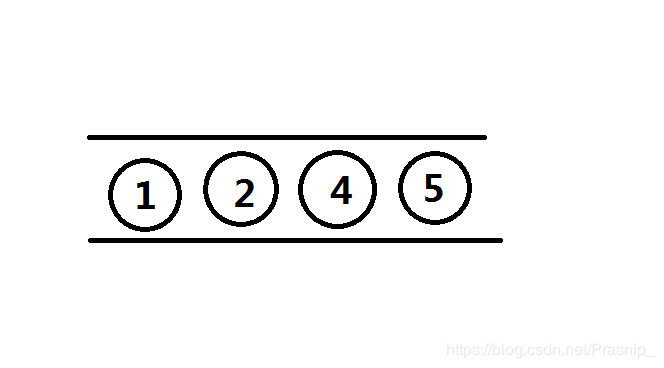
下图是一个单调递增的单调队列模型。

其中元素也是从小到大排列。
和单调栈的操作一样,如果加入一个满足单调性的元素,例如5,那么就直接加入。
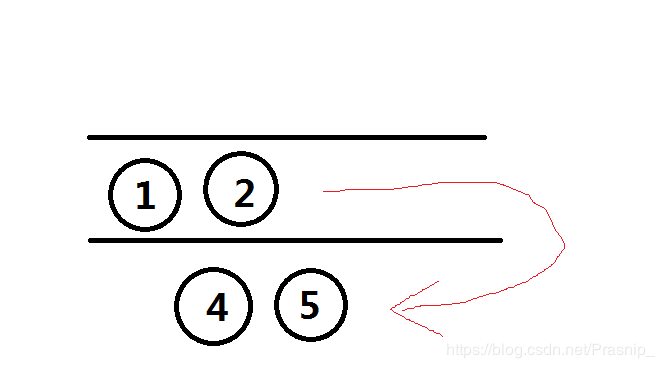
那么如果加入一个元素3呢?我们维护单调性,需要把队列尾端把大于3的元素全部弹出,那么就需要用双端队列来实现了,当然操作和单调栈是一样的。
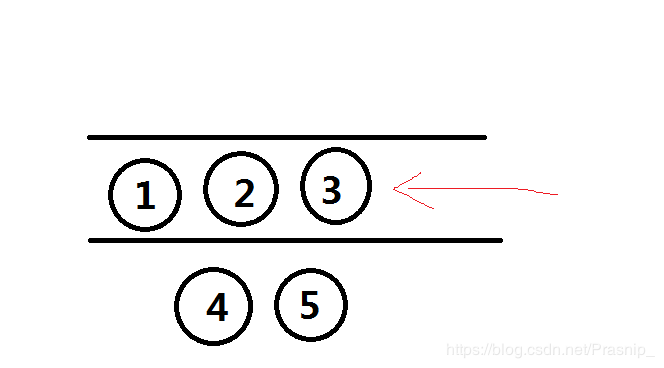
单调队列有许多作用:
比如可以求出一个数组内第一个大于等于一个数x的数
也可以通过维护单调性,解决一些区间内最小或最大的问题
总之单调队列的应用在根本上要视题目而定的灵活运用
本质上并不复杂
如果求最大,就维护单调递减的队列;如果求最小,就维护单调递增的队列
题目描述
现在有一堆数字共N个数字(N<=10^6),以及一个大小为k
的窗口。现在这个从左边开始向右滑动,每次滑动一个单
位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
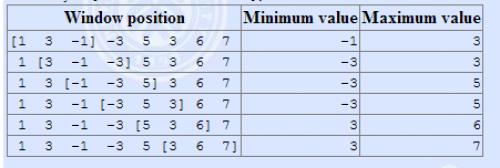
输入格式:
输入一共有两行,第一行为n,k。
第二行为n个数(<INT_MAX).
输出格式:
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
输入输出样例
输入样例#1:
8 3
1 3 -1 -3 5 3 6 7
输出样例#1:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
请用C++提交
#include <stdio.h> #include <algorithm> #include <iostream> #include <stdbool.h> #include <stdlib.h> #include <string> #include <string.h> #include <math.h> #include <vector> #include <queue> #include <stack> #include <set> #include <map> #define INF 0x3f3f3f3f #define LL long long #define MAXN 2000005 using namespace std; struct Node{ int index; int val; }; int a[MAXN]; deque<Node> q; int main() { int n,m; Node node; scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) scanf("%d",&a[i]); for (int i=1;i<=n;i++) // 区间最大值 { node.val = a[i]; node.index = i; while (!q.empty() && q.back().val<a[i]) q.pop_back(); q.push_back(node); if (i>=m) { while (!q.empty() && q.front().index+m<=i) q.pop_front(); printf("%d ",q.front().val); } } while (!q.empty()) //区间最小值 q.pop_front(); for (int i=1;i<=n;i++) { node.val = a[i]; node.index = i; while (!q.empty() && a[i]<q.back().val) q.pop_back(); q.push_back(node); if (i>=m) { if (!q.empty() && q.front().index+m<=i) q.pop_front(); printf("%d ",q.front().val); } } return 0; }