Just to remind, girls in Arpa's land are really nice.
Mehrdad wants to invite some Hoses to the palace for a dancing party. Each Hos has some weight wi and some beauty bi. Also each Hos may have some friends. Hoses are divided in some friendship groups. Two Hoses x and y are in the same friendship group if and only if there is a sequence of Hoses a1, a2, ..., ak such that ai and ai + 1 are friends for each 1 ≤ i < k, and a1 = x and ak = y.
Arpa allowed to use the amphitheater of palace to Mehrdad for this party. Arpa's amphitheater can hold at most w weight on it.
Mehrdad is so greedy that he wants to invite some Hoses such that sum of their weights is not greater than w and sum of their beauties is as large as possible. Along with that, from each friendship group he can either invite all Hoses, or no more than one. Otherwise, some Hoses will be hurt. Find for Mehrdad the maximum possible total beauty of Hoses he can invite so that no one gets hurt and the total weight doesn't exceed w.
The first line contains integers n, m and w (1 ≤ n ≤ 1000,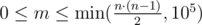 
, 1 ≤ w ≤ 1000) — the number of Hoses, the number of pair of friends and the maximum total weight of those who are invited.
The second line contains n integers w1, w2, ..., wn (1 ≤ wi ≤ 1000) — the weights of the Hoses.
The third line contains n integers b1, b2, ..., bn (1 ≤ bi ≤ 106) — the beauties of the Hoses.
The next m lines contain pairs of friends, the i-th of them contains two integers xi and yi (1 ≤ xi, yi ≤ n, xi ≠ yi), meaning that Hoses xi and yi are friends. Note that friendship is bidirectional. All pairs (xi, yi) are distinct.
Print the maximum possible total beauty of Hoses Mehrdad can invite so that no one gets hurt and the total weight doesn't exceed w.
3 1 5
3 2 5
2 4 2
1 2
6
4 2 11
2 4 6 6
6 4 2 1
1 2
2 3
7
In the first sample there are two friendship groups: Hoses {1, 2} and Hos {3}. The best way is to choose all of Hoses in the first group, sum of their weights is equal to 5 and sum of their beauty is 6.
In the second sample there are two friendship groups: Hoses {1, 2, 3} and Hos {4}. Mehrdad can't invite all the Hoses from the first group because their total weight is 12 > 11, thus the best way is to choose the first Hos from the first group and the only one from the second group. The total weight will be 8, and the total beauty will be 7.
题意：
有n个女孩，每个女孩有重量和美丽度，有m对朋友关系，朋友关系可传递。邀请他们参加聚会，每一个朋友圈的人要么全部参加，要么不参加，要么只有一个人参加。问在不超过总重量w的条件下最大美丽度是多少。
代码：
1 //显然背包，分两种物品，单个的人，整个集合的人。 2 #include<bitsstdc++.h> 3 using namespace std; 4 long long dp[1003]; 5 int hm[1003],hd[1003],vis[1003],fat[1003]; 6 int n,m,w; 7 vector<int>L[1003]; 8 int find(int x) 9 { 10 if(fat[x]!=x) 11 fat[x]=find(fat[x]); 12 return fat[x]; 13 } 14 void connect(int x,int y) 15 { 16 int xx=find(x),yy=find(y); 17 if(xx!=yy) 18 fat[yy]=xx; 19 } 20 void init() 21 { 22 for(int i=0;i<=n;i++) 23 fat[i]=i; 24 } 25 int main() 26 { 27 scanf("%d%d%d",&n,&m,&w); 28 for(int i=1;i<=n;i++) 29 scanf("%d",&hm[i]); 30 for(int i=1;i<=n;i++) 31 scanf("%d",&hd[i]); 32 int x,y; 33 init(); 34 for(int i=0;i<m;i++) 35 { 36 scanf("%d%d",&x,&y); 37 connect(x,y); 38 } 39 memset(vis,0,sizeof(vis)); 40 int cnt=0; 41 for(int i=1;i<=n;i++) 42 { 43 int tem=find(i); 44 if(!vis[tem]) 45 { 46 L[++cnt].push_back(tem); 47 if(tem!=i) 48 L[cnt].push_back(i); 49 vis[tem]=cnt; 50 } 51 else if(vis[tem]&&tem!=i) 52 { 53 L[vis[tem]].push_back(i); 54 } 55 } 56 memset(dp,0,sizeof(dp)); 57 for(int i=1;i<=cnt;i++) 58 { 59 int len=L[i].size(); 60 long long sum1=0,sum2=0; 61 for(int j=0;j<len;j++) 62 { 63 sum1+=hm[L[i][j]]; 64 sum2+=hd[L[i][j]]; 65 } 66 for(int k=w;k>=0;k--) 67 { 68 if(k>=sum1) //整个集合的 69 dp[k]=max(dp[k],dp[k-sum1]+sum2); 70 for(int j=0;j<len;j++) //单个的 71 { 72 int tem=L[i][j]; 73 if(k>=hm[tem]) 74 dp[k]=max(dp[k],dp[k-hm[tem]]+hd[tem]); 75 } 76 } 77 } 78 cout<<dp[w]<<endl; 79 return 0; 80 }