2018-2019 ACM-ICPC Nordic Collegiate Programming Contest (NCPC 2018)-E. Explosion Exploit-概率+状压dp
【Problem Description】
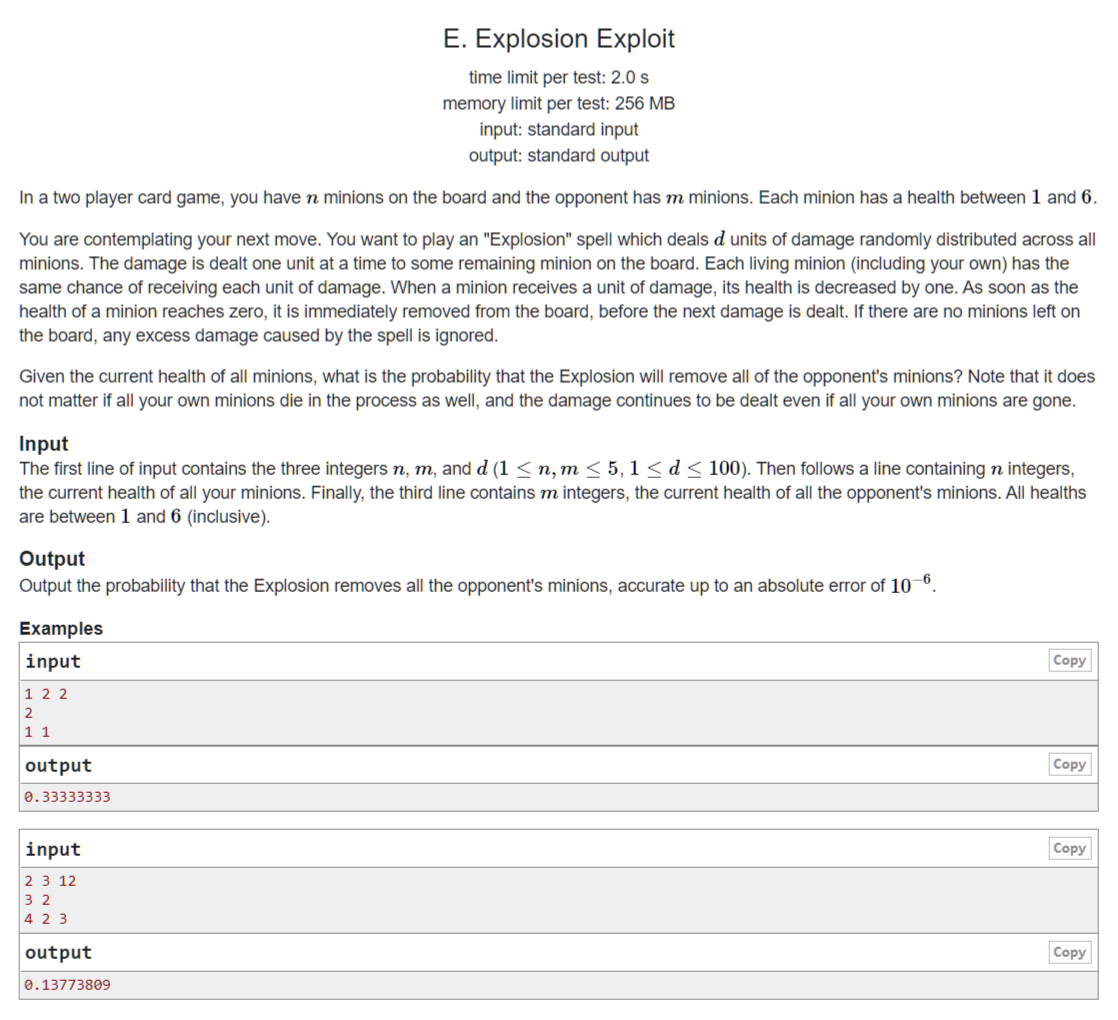
我方有(n)个人,对方有(m)个人,每个人都有一个健康值(h_i),有(d)次攻击,每次随机从所有人中选(1)个人,减少其(1)健康值。问将对方所有人都消灭的概率是多少?
【Solution】
方法(1):
将所有人的健康值作为一种状态,因为(h)最大为(6),所以可以将所有人的健康值状态通过(7)进制数(hash)成一个整数,便于保存以及状态的转移。假设目前的状态(hash)值为(state),健康值大于(0)的人数有(sz)个,枚举所有可能选择的人,对于其中一个人,使其健康值减(1)后的状态为(nextstate),则有(dp[nextstate]=dp[state] imes frac{1}{sz})。经过(d)次之后所有状态中,将对方人数为(0)的概率加起来即可。
但是有几个问题:
- 最多会有(10)个人,所以可能需要(7^{10}=3 imes 10^8)来保存状态,存不下,但是可以发现,存储状态的时候,与所有人的健康值的大小顺序无关,所以可以强制保证他们有序。这样只需要(2 imes 10^5)。
- 转换为(7)进制且每个状态都对其排序后,最终无法知道那些人是对方的人。可以在保存的时候,将对方的人的健康值取负,这样排序后对方的人一定排在最前端。转换进制也改变为(13)进制,且对于每个人的健康值增加(6)的偏移值,保证健康值都是正数。这样最终只要判断一下最前端的人的健康值是否大于(0)即可。
方法(2):
根据健康值分类,统计每种健康值的人数(己方与对方的人分开统计),然后将(6)种健康值对应的人数也通过(7)进制数(hash)到一个整数上,加上对方的人总共最多需要(12)位,且高位存储对方每种健康值的人数,这样可以通过判断(state)是否小于等于(all=(666666)_7),来确定对方的人是否全被消灭。
然后就是转移,枚举健康值(i),每次从健康值为(i)的人里选(1)个人,将其健康值减(1),选择健康值为(i)的人的概率为(frac{h[i]}{sum}),其中(h[i])为,健康值为(i)的人数,(sum)为总人数。所以有(dp[state]=dp[nextstate]*frac{h[i]}{sum})。
【Code】
//方法1
#include<iostream>
#include<iomanip>
#include<map>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
#define int long long
map<int,double>dp; //dp[state]表示从初始状态转换到状态state的概率为dp[state]
vector<int>v;
int encode(vector<int>v){ //hash为13进制
int ans=0,tmp=1;
for(auto vv:v){
ans+=(vv+6)*tmp; //增加6的偏移值,保证都为正数
tmp*=13;
}
return ans;
}
vector<int> decode(int state){ //求每个人的健康值
v.clear();
while(state){
v.push_back(state%13-6);
state/=13;
}
sort(v.begin(),v.end()); //保证有序
return v;
}
map<int,double> solve(){
map<int,double>mp;
for(auto v:dp){
vector<int>state=decode(v.first);
for(int i=0;i<state.size();i++){ //枚举每种选择,转移状态
vector<int>copy(state);
if(copy[i]>0) copy[i]--;
else if(copy[i]<0) copy[i]++;
if(copy[i]==0){ //将健康值为0的人去除
copy.erase(copy.begin()+i);
}else{
sort(copy.begin(),copy.end()); //保证健康值有序
}
mp[encode(copy)]+=v.second*1.0/state.size();
}
}
return mp;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n,m,d,sum1=0;cin>>n>>m>>d;
for(int i=1;i<=n;i++){
int x;cin>>x;sum1+=x;
v.push_back(x);
}
int sum2=0;
for(int i=1;i<=m;i++){
int x;cin>>x;sum2+=x;
v.push_back(-x); //将对方的人健康值取负,以在最终的时候区别我方/对方
}
if(sum2>d){ //无法将对方所有人都消灭
cout<<"0"<<endl;
return 0;
}
if(sum1+sum2<=d){ //可将所有人都消灭
cout<<"1"<<endl;
return 0;
}
sort(v.begin(),v.end()); //保证有序
dp[encode(v)]=1;
for(int i=0;i<d;i++) dp=solve(); //转移d次
double ans=0;
for(auto v:dp){
vector<int>t=decode(v.first);
if(t.size()&&t[0]>0) ans+=v.second; //如果最小的人的健康值都大于0,则对方的人一定都被消灭
}
cout<<setiosflags(ios::fixed)<<setprecision(9);
cout<<ans<<endl;
return 0;
}
//方法2
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<map>
using namespace std;
#define maxn 10
#define INF 0x3f3f3f3f
#define int long long
int h1[maxn]/*己方健康值为i的人数*/,h2[maxn]/*对方健康值为i的人数*/,all=0/*临界值*/;
int encode(){
int ans=0;
for(int i=1;i<=6;i++) ans=ans*7+h2[i]; //对方放在高6位
for(int i=1;i<=6;i++) ans=ans*7+h1[i]; //己方放在低6位
return ans;
}
map<int,double>dp;
double dfs(int pos,int state){
if(dp.count(state)) return dp[state];
double &ans=dp[state],sum=0;
if(state<=all) return ans=1; //如果高6位全为0,则对方全被消灭
if(pos==0) return ans=0;
for(int i=1;i<=6;i++){
if(!h1[i]) continue;
sum+=h1[i]; //总人数
h1[i]--;h1[i-1]++; //当前血量的人减少一个,前一个血量的人增加一个,使得总血量只减少了1
ans+=(h1[i]+1)*dfs(pos-1,encode());
h1[i]++;h1[i-1]--; //注意恢复
}
for(int i=1;i<=6;i++){
if(!h2[i]) continue;
sum+=h2[i];
h2[i]--;h2[i-1]++;
ans+=(h2[i]+1)*dfs(pos-1,encode());
h2[i]++;h2[i-1]--;
}
ans/=sum; //最后除以总人数
return ans;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n,m,d;cin>>n>>m>>d;
for(int i=1;i<=n;i++){
int x;cin>>x;h1[x]++;
}
for(int i=1;i<=m;i++){
int x;cin>>x;h2[x]++;
}
for(int i=1;i<=6;i++) all=all*7+6; //低6位全满时的最大值
cout<<setiosflags(ios::fixed)<<setprecision(9);
cout<<dfs(d,encode())<<endl;
return 0;
}