title: 线段树相关
date: 2019-07-30 15:23:00
tags: [undone]
mathjax: true
toc: true
线段树是一种神奇的数据结构,能将区间数据多次修改与多次求和的复杂度降低,而且它还有升级版
线段树 (I)
产生背景
假设我们有(n)个要处理的数据

有两种处理操作方式,一种是单点修改某个数据的值,另一个是对于区间(l ~ r)进行求和。这两种操作都要进行(n)次

对于一系列数字元素存储在数组中,我们想进行多次单点修改操作和多次区间求和操作,一般有两种方法
一是直接进行模拟操作,每一次单点修改耗费(O(1))的时间,每一次区间求和耗费(O(n))的时间。总共时间复杂度为(O(n^2))

另外一种就是用前缀和进行优化,能够将每次区间求和耗费时间由(O(n))降低到(O(1)),但是每次单点修改的耗费时间却变成了(O(n)),总共时间复杂度为(O(n^2))
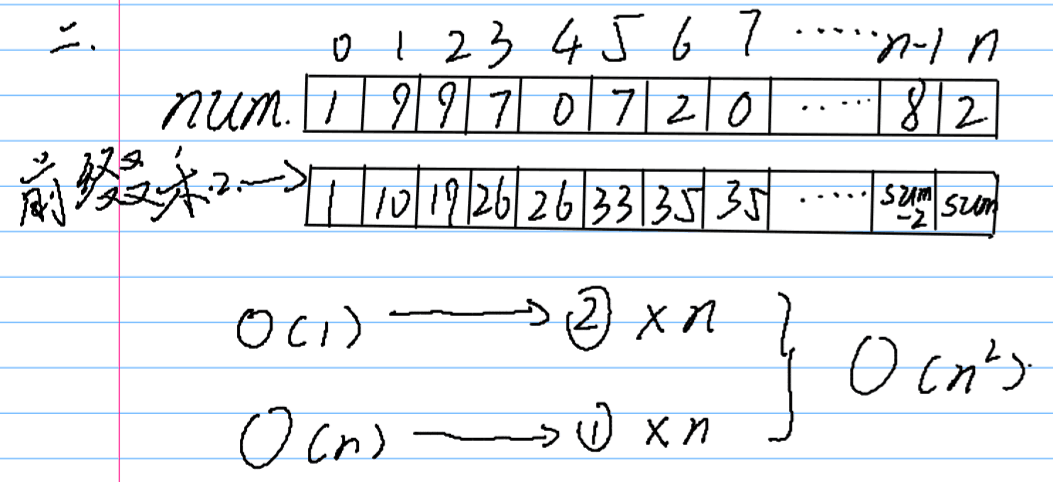
这个时候,线段树要上场了。
原理
线段树的原理是就是分治区间和,将一个大区间分成两个小区间,两个小区间分成四个小小区间......

对于每一个单点修改,只会消耗(log n)的时间;每一次区间求和,也只用消耗(log n)的时间
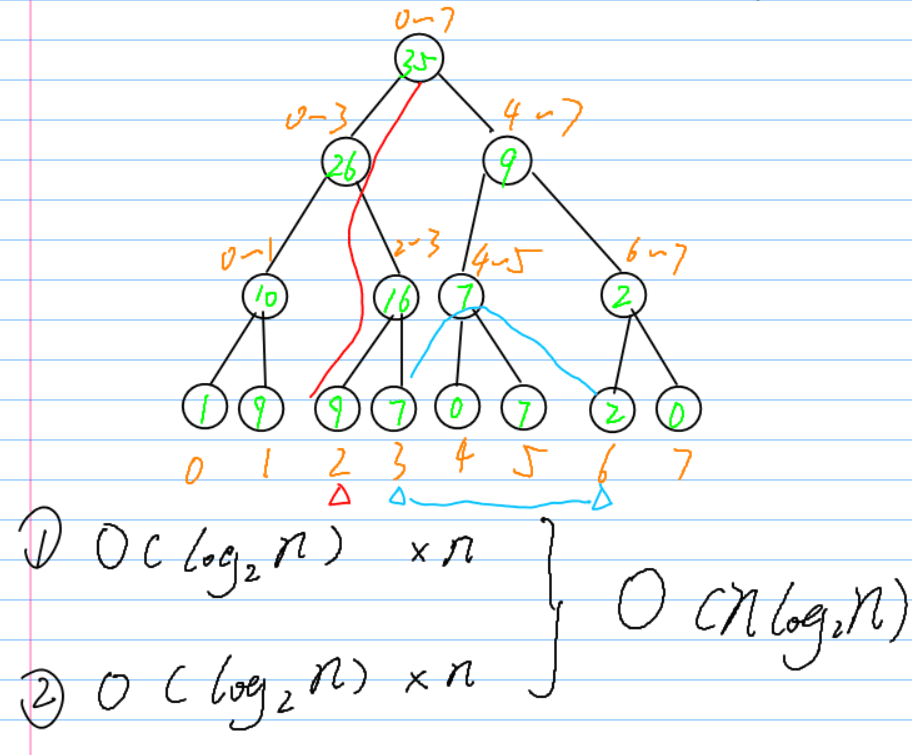
这样就大大的优化了时间复杂度
题目:P3374 【模板】树状数组 1
虽然这题叫做树状数组的模板题,但是也是线段树的最简单的模板题
/*
*@Author: ChenShou
*@Language: C++
*/
//#include <bits/stdc++.h>
#include<iostream>//
#include<algorithm>//
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<string>
#include<vector>//
#include<bitset>
#include<queue>
#include<deque>
#include<stack>
#include<cmath>
#include<list>
#include<map>
#include<set>
//#define DEBUG
#define RI register int
#define endl "
"
using namespace std;
typedef long long ll;
//typedef __int128 lll;
const int N=100000+10;
const int M=100000+10;
const int MOD=1e9+7;
const double PI = acos(-1.0);
const double EXP = 1E-9;
const int INF = 0x3f3f3f3f;
const int maxn = 1e5+6;
int arr[maxn*10],m,n;
int tree[ maxn*40 ]={0};
void build_tree( int arr[] , int tree[] , int node , int start , int end ) {
if( start == end ){
tree[node] = arr[start];
}
else {
int mid = ( start + end ) >> 1 ;
int left_node = ( node << 1 ) + 1 ;
int right_node = ( node << 1 ) + 2 ;
build_tree(arr, tree, left_node , start, mid ) ;
build_tree(arr, tree, right_node, mid+1, end ) ;
tree[node] = tree[left_node] + tree[right_node] ;
}
}
void update_tree(int arr[],int tree[],int node,int start,int end,int idx ,int val){
if( start == end ){
arr[idx] += val;
tree[node] += val;
}
else {
int mid = (start+end) >> 1 ;
int left_node = ( node << 1) + 1 ;
int right_node = ( node << 1) + 2 ;
if(idx >= start && idx <= mid )
update_tree(arr,tree,left_node,start,mid,idx,val);
else
update_tree(arr,tree,right_node,mid+1,end,idx,val);
tree[node] = tree[left_node] + tree[right_node] ;
}
}
int sum_tree(int arr[], int tree[], int node, int start, int end, int L, int R){
if( R < start || L > end )
return 0;
else if(L<=start&&end<=R)
return tree[node];
else if(start==end)
return tree[node];
else {
int mid = ( start + end ) >> 1 ;
int left_node = (node<<1) + 1 ;
int right_node = (node<<1) + 2;
int sum_left=sum_tree(arr,tree,left_node,start,mid,L,R);
int sum_right=sum_tree(arr,tree,right_node,mid+1,end,L,R);
return sum_left+sum_right;
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 0 ; i < n ; i++ ){
scanf("%d",&arr[i]);
}
build_tree(arr, tree, 0, 0, n-1 );
for(int i=0 ; i<m ; i++){
int o,a,b;
scanf("%d",&o);
if(o==1){
scanf("%d %d",&a,&b);
update_tree(arr,tree,0,0,n-1,a-1,b);
}
else {
scanf("%d %d",&a,&b);
printf("%d
",sum_tree(arr,tree,0,0,n-1,a-1,b-1));
}
}
return 0;
}
题目:I Hate It
一个小变形,单点修改,区间求和变为区间求最大值。
#include<bits/stdc++.h>
using namespace std;
void build_tree ( int arr[] , int tree[] , int node , int start , int end ){
if( start == end ) {
tree[node] = arr[start];
}
else {
int mid = ( start + end ) >>1;
int left_node = ( node<<1 ) + 1 ;
int right_node = ( node<<1 ) + 2 ;
build_tree(arr, tree, left_node , start , mid );
build_tree(arr, tree, right_node, mid+1 , end );
tree[node] = max( tree[left_node] , tree[right_node] );
}
}
void update_tree ( int arr[] , int tree[] , int node , int start , int end , int idx , int val ) {
if(start == end){
arr[idx] = val;
tree[node] = val;
}
else {
int mid = ( start+end ) >> 1;
int left_node = ( node << 1 ) + 1 ;
int right_node = ( node << 1 ) + 2 ;
if(idx>=start&&idx<=mid){
update_tree(arr,tree,left_node,start,mid,idx,val);
}
else {
update_tree(arr,tree,right_node,mid+1,end,idx,val);
}
tree[node] = max ( tree[left_node] , tree[right_node] ) ;
}
}
int max_tree( int arr[] , int tree[] , int node , int start , int end , int L , int R ) {
if ( R<start || L>end ) {
return 0 ;
}
else if( L<=start&&end<=R) {
return tree[node] ;
}
else if (start==end) {
return tree[node] ;
}
else {
int mid = ( start + end ) >> 1 ;
int left_node = ( node << 1 ) + 1 ;
int right_node = ( node << 1 ) + 2 ;
int max_left = max_tree ( arr , tree , left_node , start , mid , L , R ) ;
int max_right = max_tree ( arr , tree , right_node, mid+1 , end , L , R ) ;
return max ( max_left , max_right ) ;
}
}
int num[2000000+7]={0};
int tree[1<<19]={0};
int main(){
int n,q;
while(scanf("%d %d",&n,&q)!=EOF){
for(int i=0;i<n;i++)scanf("%d",&num[i]);
build_tree(num,tree,0,0,n-1);
for(int ii=0;ii<q;ii++){
char o[10];
int l,r,i,b;
scanf("%s",o);
if(o[0]=='Q'){
scanf("%d %d",&l,&r);
printf("%d
", max_tree( num , tree , 0 , 0 , n-1 , l-1 , r-1 ));
}else {
scanf("%d %d",&i,&b);
update_tree ( num , tree , 0 , 0 , n-1 , i-1 , b );
}
}
}
return 0;
}
线段树 ( II )
产生背景
普通的单点修改,区间求和已经实现了。但是如果我们要区间修改怎么办?把区间修改转换为单点修改?往往会TLE.....
这个时候,带有lazy标签的线段树就要上场了
原理
对于每一次的区间修改,如果能够在区间节点上记录这个区间的数全部进行某一种操作,那么往往可以节约很多时间。
题目 P3372 【模板】线段树 1
别人的代码
#include<iostream>
#include<cstdio>
#define MAXN 1000007
#define ll long long
using namespace std;
unsigned ll n,m,a[MAXN],ans[MAXN<<2],tag[MAXN<<2];
ll ls(ll x)
{
return x*2;
}
ll rs(ll x)
{
return x*2+1;
}
void scan()
{
cin>>n>>m;
for(ll i=1;i<=n;i++)
scanf("%lld",&a[i]);
}
void push_up(ll p)
{
ans[p]=ans[ls(p)]+ans[rs(p)];
}
void build(ll p,ll l,ll r)
{
tag[p]=0;
if(l==r){ans[p]=a[l];return ;}
ll mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
push_up(p);
}
void f(ll p,ll l,ll r,ll k)
{
tag[p]=tag[p]+k;
ans[p]=ans[p]+k*(r-l+1);
}
void push_down(ll p,ll l,ll r)
{
ll mid=(l+r)>>1;
f(ls(p),l,mid,tag[p]);
f(rs(p),mid+1,r,tag[p]);
tag[p]=0;
}
void update(ll nl,ll nr,ll l,ll r,ll p,ll k)
{
if(nl<=l&&r<=nr)
{
ans[p]+=k*(r-l+1);
tag[p]+=k;
return ;
}
push_down(p,l,r);
ll mid=(l+r)>>1;
if(nl<=mid)update(nl,nr,l,mid,ls(p),k);
if(nr>mid) update(nl,nr,mid+1,r,rs(p),k);
push_up(p);
}
ll query(ll q_x,ll q_y,ll l,ll r,ll p)
{
ll res=0;
if(q_x<=l&&r<=q_y)return ans[p];
ll mid=(l+r)>>1;
push_down(p,l,r);
if(q_x<=mid)res+=query(q_x,q_y,l,mid,ls(p));
if(q_y>mid) res+=query(q_x,q_y,mid+1,r,rs(p));
return res;
}
int main()
{
ll a1,b,c,d,e,f;
scan();
build(1,1,n);
while(m--)
{
scanf("%lld",&a1);
switch(a1)
{
case 1:{
scanf("%lld%lld%lld",&b,&c,&d);
update(b,c,1,n,1,d);
break;
}
case 2:{
scanf("%lld%lld",&e,&f);
printf("%lld
",query(e,f,1,n,1));
break;
}
}
}
return 0;
}
题目 P3373 【模板】线段树 2
权值线段树
产生背景
为了过渡线段树和主席树之间的鸿沟 ,这里讲一下权值线段树
原理
权值线段树,就是 权值 + 线段树 。线段树我们已经知道是什么了 , 那么权值指的是什么?
中学阶段我们都学了平均数 , 还有加权平均数 。 权值就是指占的比重不同 。 在权值线段树里面 , 权值指的是 数据 出现的次数。
或者这么说 权值线段树之所以会带上“权值”二字,是因为它是记录权值的线段树。因此需要用到离散化操作来处理a[1-n]。记录权值指的是,每个点上存的是区间内的数字出现的总次数。比如一个长度为10的数组[1,1,2,3,3,4,4,4,4,5]。
如图 :

那么刚刚提到的离散化是什么?
离散化,其实是指将较为松散的数据范围通过某种处理将数据集中但不改变其大小关系从而实现数据存储的压缩
比如10的数组[1,1,20,300,300,4000,4000,4000,4000,50000]
就可以类似处理为[1,1,2,3,3,4,4,4,4,5]
题目
主席树
产生背景
原理
题目 $ K^{th} $ Number Feed the dogs
/*
*@Author: ChenShou
*@Language: C++
*/
//#include <bits/stdc++.h>
#include<iostream>//
#include<algorithm>//
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<string>
#include<vector>//
#include<bitset>
#include<queue>
#include<deque>
#include<stack>
#include<cmath>
#include<list>
#include<map>
#include<set>
//#define DEBUG
#define RI register int
#define endl "
"
using namespace std;
typedef long long ll;
//typedef __int128 lll;
const int N=100000+10;
const int M=100000+10;
const int MOD=1e9+7;
const double PI = acos(-1.0);
const double EXP = 1E-9;
const int INF = 0x3f3f3f3f;
const int maxn = 1e5+6;
int n,m,cnt,root[maxn],a[maxn],x,y,k;
struct node{
int l;
int r;
int sum;
}T[maxn*40];
vector < int > v ;
int getid( int x ) { //离散化
return lower_bound( v.begin() , v.end() , x ) - v.begin() +1 ;
}
void update(int l,int r,int &x,int y,int pos){ //更新
T[++cnt]=T[y];
T[cnt].sum++;
x=cnt;
if(l==r)return ;
int mid=((l+r)>>1);
if(mid>=pos)
update(l,mid,T[x].l,T[y].l,pos);
else
update(mid+1,r,T[x].r,T[y].r,pos);
}
int query(int l,int r,int x,int y,int k){ //询问
if(l==r)return l ;
int mid = (l+r)>>1;
int sum = T[T[y].l].sum - T[T[x].l].sum ;
if(sum>=k)return query(l,mid,T[x].l,T[y].l,k);
else return query(mid+1,r,T[x].r,T[y].r,k-sum);
}
int main()
{
#ifdef DEBUG
freopen("input.in", "r", stdin);
//freopen("output.out", "w", stdout);
#endif
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//scanf("%d",&t);
//while(t--){
//}
scanf ( "%d %d" , &n , &m ) ;
for( int i = 1 ; i <= n ; i++ ){
scanf ( "%d" , & a[i] ) ;
v.push_back(a[i]);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end()); //去重排序
for( int i = 1 ; i <= n ; i++ ){
update ( 1 , n , root[i] , root[i-1] , getid(a[i])) ;
}
for( int i = 1 ; i <= m ; i++ ){
scanf ( "%d %d %d" , &x , &y , &k ) ;
printf ( "%d
" , v[ query ( 1 , n , root[x-1] , root[y] , k ) - 1 ] ) ;
}
#ifdef DEBUG
printf("Time cost : %lf s
",(double)clock()/CLOCKS_PER_SEC);
#endif
//cout << "Hello world!" << endl;
return 0;
}