难得更新一次博客...
(wqs)二分:
背景(都是意外):
省选前大模拟测去年联考题,由于(Day 1)写挂写假很自闭,(Day 2)就直接胡乱莽,(T1)读题吓着了,(T3)看出来大概的思路但是不会降复杂度又懒得写(25)暴力,于是全程莽(T2)(意外的起源)。
画了几个图之后发现这个题实质是选(k+1)条链,然后考虑到选中的(k)条边相当于删去,那么如果这些边恰好都是负权边,答案在某种yy出来的意义上会增大,然后如果负权边数量小于(k),就一定会删掉正权边,答案在某种意义上就会变小(凭感觉伪证出结论...),于是就想到两星期前的某道模拟测试题,题目是要求图上最短路,路径长度定义为路径上边权前(k)大的权值和,那个题正解是二分边权最小值然后所有边权减去二分值(和(0)取(max))跑最短路,最后把最短路的(k)个二分值长度加上去(其实是我记错了,那个题枚举所有出现的长度了,实际上并没有二分),整个是一个下凸(横坐标最小边权,纵坐标最短路长度,排序之后就是求下凸的谷值)。然后就顺势想到二分一下链长,和之前的题反过来做,让损失最小分割。最后因为写错变量名,连样例都没过,偷税的爆零。
中午回来之后依旧觉得自己写的是对的,然后仔细检查发现变量名和快读都有点锅,改完之后抱着试一试的心态重新测了一次,然后,然后,然后......竟然过了(心情复杂)。中午看了一下正解,看起来我好像写的和正解思路差不多(神情恍惚),不过不是普通意义上简单的二分,而是(wqs)二分,也叫带权二分、(DP)凸优化(论一个想假的人莫名其妙一上午想到了一个神仙东西之后被乱%的心情有多复杂...胡乱莽了一上午然后还一把翻盘了...天知道我一上午干了什么...)。
好了,下面进入正题。
适用范围:
给出一个选物品的限制,然后要求恰好选(k)个,使得权值和最大/小。其中,随着选择个数的增加,权值和会呈现出单调性(上凸或下凸)。
原理:
由上凸或下凸的性质,不难发现会有如图的形状。
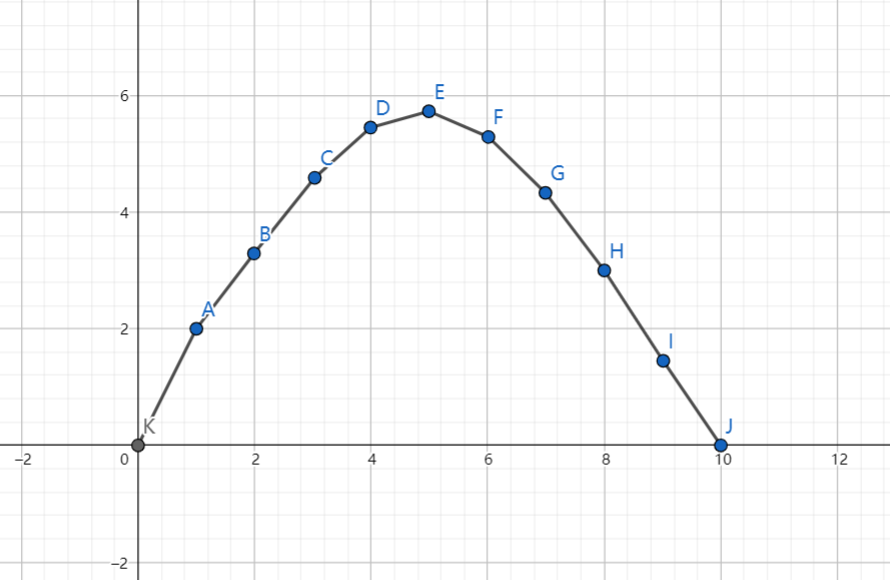
由这一点,可以发现所求的点应该是横坐标为(k)的点,当然,也只是知道了形状而已,并不知道上凸的点坐标分别是什么,于是考虑二分切线斜率,让答案点是切点,有这样的一个性质:
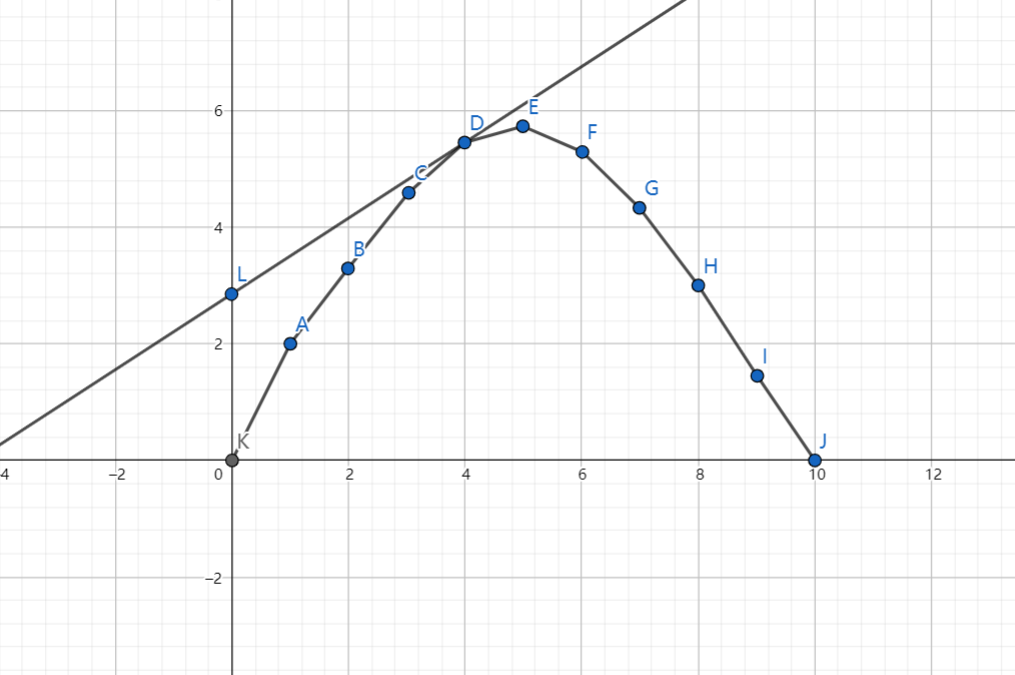
切线斜率单调不升,当切线斜率减小时,切得的点横坐标增大,反之减小,所以每次二分判断切点横坐标即可。另外还有一点:

如果斜率一定,那么过切点位置的直线(切线)截距最大,所以我们求得定斜直线在截距最大的情况下与凸包的切点横坐标就可以进行检验了。
不过还有一点需要注意,可能切线上会有多个点,也即在某个斜率的情况下有多个最优决策点,在这种情况下要取横坐标最小的决策点,最后取(x_{max})求答案。
例题:
[八省联考2018]林克卡特树lct各位都说学过(wqs)二分之后就是一眼题,对于这道题就是二分斜率,然后判断截距最大而且最优决策点横坐标最小的点的位置,二分的check(O(n))贪心求最大截距以及满足条件的最小横坐标即可。找到最小的满足切点横坐标为(k+1)(链数)的斜率,然后截距加横坐标乘斜率就是纵坐标(答案)的值。