codeforces#272 C. Dreamoon and Strings 字符串 dp
Dreamoon has a string s and a pattern string p. He first removes exactly x characters from s obtaining string s' as a result. Then he calculates 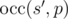 that is defined as the maximal number of non-overlapping substrings equal to p that can be found in s'. He wants to make this number as big as possible.
that is defined as the maximal number of non-overlapping substrings equal to p that can be found in s'. He wants to make this number as big as possible.
More formally, let's define 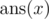 as maximum value of
as maximum value of 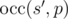 over all s' that can be obtained by removing exactly x characters froms. Dreamoon wants to know
over all s' that can be obtained by removing exactly x characters froms. Dreamoon wants to know 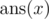 for all x from 0 to |s| where |s| denotes the length of string s.
for all x from 0 to |s| where |s| denotes the length of string s.
The first line of the input contains the string s (1 ≤ |s| ≤ 2 000).
The second line of the input contains the string p (1 ≤ |p| ≤ 500).
Both strings will only consist of lower case English letters.
Print |s| + 1 space-separated integers in a single line representing the 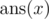 for all x from 0 to |s|.
for all x from 0 to |s|.
aaaaa
aa
2 2 1 1 0 0
axbaxxb
ab
0 1 1 2 1 1 0 0
For the first sample, the corresponding optimal values of s' after removal 0 through |s| = 5 characters from s are {"aaaaa", "aaaa","aaa", "aa", "a", ""}.
For the second sample, possible corresponding optimal values of s' are {"axbaxxb", "abaxxb", "axbab", "abab", "aba", "ab","a", ""}.
dp[i][j]为前i个字符删除j个时的匹配p的最大数目。
dp[i][j]=max(dp[i-x-m][j-x]),m为p串长度,x为s从i开始向前匹配p需要删除的字符数。


#include<bits/stdc++.h> #define REP(i,a,b) for(int i=a;i<=b;i++) #define MS0(a) memset(a,0,sizeof(a)) using namespace std; const int maxn=1000100; const int INF=(1<<29); char s[maxn],t[maxn]; int n,m; int dp[2200][2200]; int del(int k) { int res=0; int i=k,j=m; while(i>=1&&j>=1){ if(s[i]==t[j]) i--,j--; else i--,res++; } if(j==0) return res; return INF; } int main() { while(scanf("%s%s",s+1,t+1)!=EOF){ n=strlen(s+1);m=strlen(t+1); MS0(dp); REP(i,0,n){ REP(j,0,n){ if(i<j) dp[i][j]=-INF; } } for(int i=1;i<=n;i++){ int x=del(i); for(int j=0;j<=i;j++){ dp[i][j]=max(dp[i-1][j],dp[i][j]); if(j-x>=0) dp[i][j]=max(dp[i-x-m][j-x]+1,dp[i][j]); } } for(int i=0;i<=n;i++){ if(i!=n) printf("%d ",dp[n][i]); else printf("%d ",dp[n][i]); } } return 0; }