1无穷级数的基本概念和基本性质。
什么是常数项无穷级数,或称常数项级数?


什么是部分和。
![]()

什么是一般项。即un
什么是无穷级数的收敛?

其中s就是该级数的和。那什么是发散呢?

可以用一个简单的小题练练手!


这里关于,等比数列不熟,而且q的讨论其实是 |q|<1 q==1 |q|>1
然后5个性质,都非常简单。前两个和整体无穷级数有关,中间两个和部分和有关,后一个就一般项有关。
1 线性呗,2 可加性.



常数项数级的审敛法。

这是一个定理,还有一个相应的推论。

然后是一个超难的例题。


我的这个做法只有讨论p的取值时候才对了,但后面的处理p>1的时候不对。

首先要意识到,Sn是个什么东西,如何将至转换成积分。

这个就是将之转换成积分的核心。但是后面那一步就有点让我不懂了。

x究竟是什么?其实x就是 每当k取2,3,4时,取一个大于k-1 小于k的值。其中dx=1。
这样就把x和积分联系起来了。

但是如何联系起来呢?
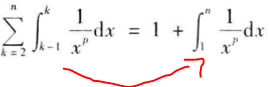
其实就是一个分解,x取k-1到k之间的某个点,带入f(x)乘以dx,并且求和,这就是积分的意义。
问题:上面这种过于特殊的化成积分的方法,是不通用的,其实比值审敛法也是可以做上题的。怎么做?
三角函数问题:一般三角函数怎么用比值审敛法,怎么用比价审敛法?有什么基本的可以比较的数级?
看了一下,三角函数,比较简单的时候用比较审敛,sinx->x , tanx -> x。复杂的时候用比值。
多项式函数问题:
一般而言,都是找他们和1/n 或者是1/n^2的比较审的极限形式关系,来解决。
但是有时候,眼尖的时候发现,如果lim(n->无穷大) un不趋进于0 的话,则发散。1/n^2则是收敛的。很少用比值。
指数函数的问题:
对于指数函数而言,发散的时候会看un是否->0,然后分类讨论正如1/1+a^n那一样。
然后指数型的用比值审敛法有着天然的容易性质。后面看到的
3^n/n2^n
n^2/3^n
2^n*n!/n^n
n*(3/4)^n
n^4/n!
这些都是用比值审敛法。
交错数级一般怎么看收敛与否?怎么看绝对收敛和条件收敛?
假如|un|发散,un收敛。那就是条件收敛。
假如|un|收敛,那么就是绝对收敛。
假如un是交错数级,1 |un+1|>|un| 2 lim(n->无穷大)un=0 的时候才是收敛。
而且要知道 1/ln(x+1) > 1/x+1。
一般而言,这里是先讨论|un| 再讨论 |un|与|un+1|的的关系。un->0吗?
幂级数
1幂级数有个问题就是要求某个幂级数的收敛区间,求收敛区间一般用阿贝尔比值法。在哪些情况下要巧妙地运用此法则呢
普通的阿贝尔法就不说了。关键是这种变形的阿贝尔法,当N=2n+1什么的时候,就选择把整个包括x也算进去。然后讨论x的取值。
或者是把f(x)=t,算t^n的收敛区间。从而算x的收敛区间。这个时候把x^2n-2拉出去x^2。变成x^2n就好了。
2还有通过逐项求导法,和逐项积分法。求得和函数。有哪些情况下是要求导,有哪些情况下是要求积分?
这里的两个特殊的积分不要忘记。