We'll call a set of positive integers a beautiful if the following condition fulfills: for any prime p, if 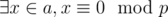 , then
, then  . In other words, if one number from the set is divisible by prime p, then at least half of numbers from the set is divisible by p.
. In other words, if one number from the set is divisible by prime p, then at least half of numbers from the set is divisible by p.
Your task is to find any beautiful set, where the number of elements is equal to k and each element doesn't exceed 2k2.
The first line contains integer k (10 ≤ k ≤ 5000) that shows how many numbers the required beautiful set should have.
In the first line print k space-separated integers that are a beautiful set. If there are multiple such sets, you are allowed to print any of them.
10
16 18 24 27 36 48 54 72 108 144
思路:贪心+dfs;
因为每个出现的素数都要在集合中至少有(n+1)/2个与他不互质的数,你可以发现所有的素数都小于17,那么也就是那些数最多就会由6个素数构成,那么我们每次贪心优先选每个素数都是那个数的因子的数就行,还有选数不能超过某个范围,所以我们先以某个数结尾,从小到大dfs找到那个至少有n个数的那个结束的素数,然后以他结尾再dfs一遍取前n个数就是答案。
1 #include<stdio.h> 2 #include<algorithm> 3 #include<stdlib.h> 4 #include<iostream> 5 #include<string.h> 6 #include<queue> 7 #include<math.h> 8 typedef long long LL; 9 using namespace std; 10 LL prime[7]= {2,3,5,7,11,13}; 11 LL ans[10000]; 12 LL ak=0; 13 LL N; 14 LL v; 15 int flag[7]; 16 int maxx_fl[7]; 17 void dfs(LL top,LL d,LL ap,bool fla) 18 { if( ap > 2*v*v)return ; 19 else if(d == -1&&fla) 20 { 21 int i,j; 22 ans[ak++]=ap; 23 return ; 24 } 25 else if(d == -1) 26 { 27 ak++; 28 return ; 29 } 30 31 else 32 { 33 LL cf=top; 34 LL as=ap; 35 while(cf > prime[d]) 36 { 37 cf /= prime[d]; 38 as *= prime[d]; 39 flag[d]++; 40 dfs(cf,d-1,as,fla); 41 } 42 dfs(top,d-1,ap,fla); 43 } 44 } 45 int main(void) 46 { 47 LL n; 48 while(scanf("%I64d",&n)!=EOF) 49 { 50 memset(flag,0,sizeof(flag)); 51 LL i,j; 52 ak=0; 53 v=n; 54 for(i=0; i<=5; i++) 55 { 56 ak=0;dfs(2*n*n,i,1,false); 57 if(ak>=v) 58 {break;} 59 } 60 ak=0; 61 dfs(2*n*n,i,1,true); 62 printf("%I64d",ans[0]); 63 for(i=1; i<n; i++) 64 printf(" %I64d",ans[i]); 65 printf(" "); 66 } 67 return 0; 68 }